深度学习神经网络训练中损失函数的选择

• 0
• 2020-05-11
• 机器学习
• 1
• 0

深度学习神经网络采用随机梯度下降优化算法进行训练。

作为优化算法的一部分，必须重复估计模型当前状态的误差。这需要选择通常称为损失函数的误差函数，该误差函数可用于估计模型的损失，以便可以更新权重以减少下一次评估时的损失。

神经网络模型从示例中学习从输入到输出的映射，并且损失函数的选择必须与特定预测建模问题(例如分类或回归)的框架相匹配。此外，输出层的配置也必须适合所选的损耗函数。

在本教程中，你将了解如何为给定预测建模问题的深度学习神经网络选择损失函数。

完成本教程后，你将了解：

• 如何为回归问题配置均方误差和变量模型。
• 如何为二进制分类配置交叉熵和铰链损失函数的模型。
• 如何为多类分类配置交叉熵和KL发散损失函数的模型。

我们开始吧。

教程概述

本教程分为三个部分；它们是：

• 回归损失函数。
  • 均方误差损失。
  • 均方对数误差损失。
  • 平均绝对误差损失。
• 二分类损失函数。
  • 二元交叉熵。
  • 铰链损失。
  • 平方铰链损失。
• 多类分类损失函数。
  • 多类交叉熵损失。
  • 稀疏多类交叉熵损失。
  • Kullback Leibler发散损失。

我们将重点讨论如何选择和实施不同的损失函数。

有关损失函数的更多理论，请参阅帖子：

• 用于训练深度学习神经网络的损失函数

回归损失函数

回归预测建模问题涉及预测实值数量。

在本节中，我们将研究适用于回归预测建模问题的损失函数。

作为本研究的上下文，我们将在make_regregation()函数中使用scikit-learn库提供的标准回归问题生成器。此函数将从具有给定数量的输入变量、统计噪声和其他属性的简单回归问题生成示例。

我们将使用此函数定义一个具有20个输入特征的问题；其中10个特征是有意义的，10个特征是不相关的。总共将随机生成1000个示例。伪随机数生成器将得到修复，以确保每次运行代码时都会得到相同的1000个示例。

# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)

当实值输入和输出变量要缩放到合理范围时，神经网络通常表现得更好。对于这个问题，每个输入变量和目标变量都具有高斯分布；因此，需要对这种情况下的数据进行标准化。

我们可以使用StandardScaler转换器类来实现这一点，这些类也来自scikit-learn库。在真正的问题上，我们将在训练数据集上准备缩放器，并将其应用于训练集和测试集，但为了简单起见，我们将在拆分成训练集和测试集之前一起缩放所有数据。

# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]

一旦进行了扩展，数据将被平均分割为训练集和测试集。

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

为了解决这一问题，将定义一个小型多层感知器(MLP)模型，并为探索不同的损失函数提供基础。

根据问题的定义，该模型将期望20个特征作为输入。该模型将有一个具有25个节点的隐藏层，并将使用校正的线性激活函数(ReLU)。在给定要预测的一个实值的情况下，输出层将具有1个节点，并且将使用线性激活函数。

# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))

该模型将符合随机梯度下降，学习率为0.01，动量为0.9，这两个值都是合理的默认值。

训练将进行100个时期，测试集将在每个时期结束时进行评估，以便我们可以在运行结束时绘制学习曲线。

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

现在我们已经有了问题和模型的基础，我们可以看一看评估适用于回归预测建模问题的三个常见损失函数。

虽然在这些示例中使用了MLP，但是在训练用于回归的CNN和RNN模型时也可以使用相同的损失函数。

均方误差损失

均方误差(MSE)损失是用于回归问题的默认损失。

在数学上，如果目标变量的分布是高斯的，则它是最大似然推理框架下的首选损失函数。它是首先评估的损失函数，只有在有充分理由的情况下才会更改。

均方误差计算为预测值和实际值之间的平方差的平均值。无论预测值和实际值的符号如何，结果始终为正，完美值为0.0。平方意味着较大的错误比较小的错误导致更多的错误，这意味着模型会因为犯较大的错误而受到惩罚。

通过在编译模型时指定‘mse’或‘mean_squared_error’作为损失函数，可以在Keras中使用均方误差损失函数。

model.compile(loss='mean_squared_error')

建议输出层具有一个用于目标变量的节点，并使用线性激活函数。

model.add(Dense(1, activation='linear'))

下面列出了关于所描述的回归问题的MLP演示的完整示例。

# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_error', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的均方误差。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到模型学习的问题实现了零误差，至少到了小数点后三位。

Train: 0.000, Test: 0.001

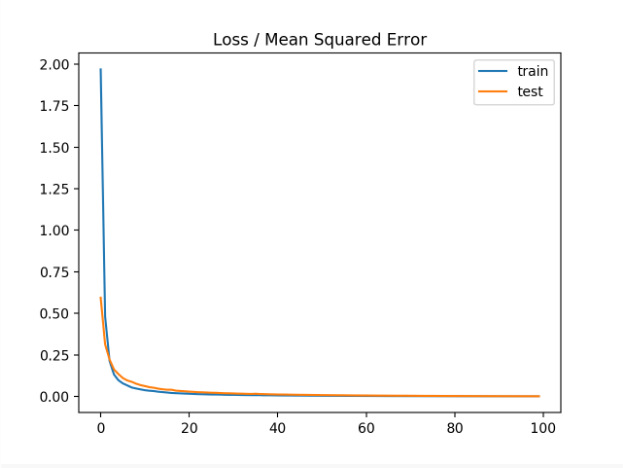
还创建了线条图，显示训练(蓝色)和测试(橙色)集合在训练时段上的均方误差损失。

我们可以看到，模型收敛得相当快，训练性能和测试性能保持相当。模型的性能和收敛行为表明均方误差是学习这一问题的神经网络的很好匹配。

均方对数误差损失

可能存在回归问题，其中目标值具有值的分布，并且在预测较大值时，你可能不想像均方误差那样严厉地惩罚模型。

相反，你可以先计算每个预测值的自然对数，然后再计算均方误差。这称为均方对数误差损失，简称MSLE。

具有缓解大预测值差异大的惩罚效果的作用。

作为损失度量，当模型直接预测未缩放的数量时，它可能更合适。不过，我们可以使用简单的回归问题来演示此损失函数。

可以更新模型以使用‘mean_squared_logarithmic_error’损失函数，并为输出层保持相同的配置。在拟合模型时，我们还将跟踪均方误差作为度量，以便我们可以将其用作性能度量，并绘制学习曲线。

model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])

下面列出了使用MSLE损失函数的完整示例。

# mlp for regression with msle loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的均方误差。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到该模型在训练和测试数据集上的MSE都略差。由于目标变量的分布是标准的高斯分布，因此它可能不太适合这个问题。

Train: 0.165, Test: 0.184

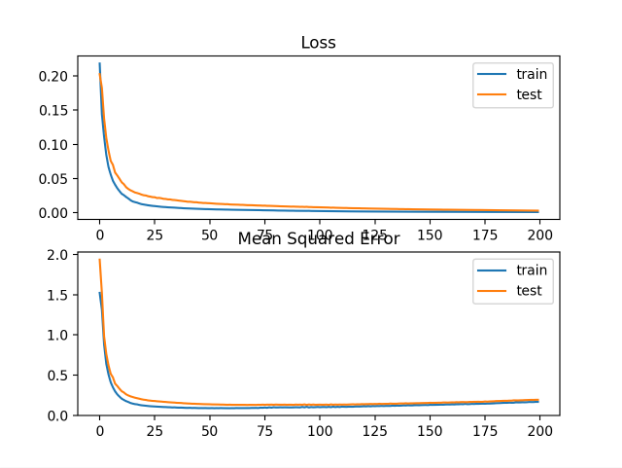
还创建了显示训练(蓝色)和测试(橙色)集合(顶部)在训练时段上的均方对数误差损失的线状图，以及用于均方误差(底部)的类似曲线图。

我们可以看到，MSLE在100 epoch的算法上收敛得很好；看起来MSE可能显示出过度拟合问题的迹象，快速下降，并从20 epoch开始上升。

平均绝对误差损失

在一些回归问题中，目标变量的分布可能大多是高斯的，但也可能有离群值，例如远离平均值的大值或小值。

在这种情况下，平均绝对误差或MAE损失是一个合适的损失函数，因为它对异常值更稳健。它被计算为实际值和预测值之间的绝对差值的平均值。

可以更新模型以使用‘mean_absolute_error’损失函数，并为输出层保持相同的配置。

model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])

下面列出了使用平均绝对误差作为回归测试问题的损失函数的完整示例。

# mlp for regression with mae loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_mse = model.evaluate(trainX, trainy, verbose=0)
_, test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot mse during training
pyplot.subplot(212)
pyplot.title('Mean Squared Error')
pyplot.plot(history.history['mean_squared_error'], label='train')
pyplot.plot(history.history['val_mean_squared_error'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的均方误差。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到模型学习了问题，实现了接近零的误差，至少到了小数点后三位。

Train: 0.002, Test: 0.002

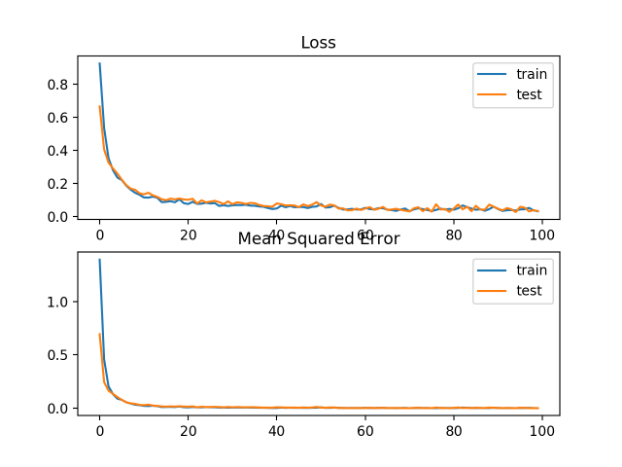
还创建了显示训练(蓝色)和测试(橙色)集(顶部)在训练时段上的平均绝对误差损失的线状图，以及用于均方误差(底部)的类似曲线图。

在这种情况下，我们可以看到MAE确实收敛了，但呈现出一个坎坷的过程，尽管MSE的动力学似乎没有受到太大的影响。我们知道目标变量是没有大的异常值的标准高斯，所以MAE在这种情况下不是很好的拟合。

如果我们不先缩放目标变量，在这个问题上可能会更合适。

二分类损失函数

二分分类是那些预测建模问题，其中示例被分配到两个标签中的一个。

该问题通常被框定为预测第一类或第二类的值0或1，并且通常被实现为预测示例属于类值1的概率。

在本节中，我们将研究适合于二分类预测建模问题的损失函数。

我们将从scikit-learn中的圆圈测试问题中生成示例，作为本次调查的基础。圆问题涉及从二维平面上的两个同心圆中提取样本，其中外圆上的点属于0类，内圆上的点属于1类。统计噪声被添加到样本中以增加歧义，并使问题更难学习。

我们将生成1000个示例，并添加10%的统计噪声。伪随机数生成器将以相同的值作为种子，以确保我们始终获得相同的1,000个示例。

# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)

我们可以创建数据集的散点图，以了解我们正在建模的问题。下面列出了完整的示例。

# scatter plot of the circles dataset with points colored by class
from sklearn.datasets import make_circles
from numpy import where
from matplotlib import pyplot
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# select indices of points with each class label
for i in range(2):
	samples_ix = where(y == i)
	pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i))
pyplot.legend()
pyplot.show()

运行该示例将创建示例的散点图，其中输入变量定义点的位置，类值定义颜色，0级为蓝色，1级为橙色。

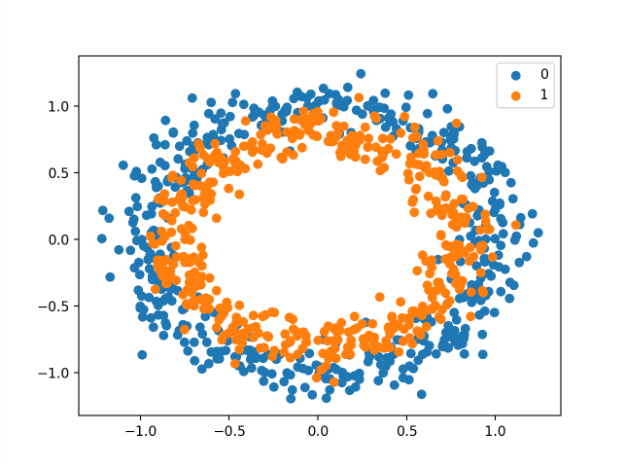
这些点已经在0附近进行了合理缩放，几乎在[-1，1]范围内。在这种情况下，我们不会重新定标。

对于训练集和测试集，数据集被平均拆分。

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

可以定义简单的MLP模型来解决该问题，该模型预期数据集中的两个特征的两个输入、具有50个节点的隐藏层、校正的线性激活函数和将需要配置用于选择损失函数的输出层。

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='...'))

模型将采用随机梯度下降进行拟合，敏感的默认学习率为0.01，动量为0.9。

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

我们将对模型进行200个训练周期的拟合，并针对每个周期结束时的损失和精度来评估模型的性能，以便绘制学习曲线。

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

现在我们有了问题和模型的基础，我们可以看一看评估适用于二分类预测建模问题的三个常见损失函数。

虽然在这些示例中使用了MLP，但是当训练用于二进制分类的CNN和RNN模型时，可以使用相同的损失函数。

二元交叉熵损失

交叉熵是用于二进制分类问题的默认损失函数。

它用于目标值位于集合{0，1}中的二进制分类。

从数学上讲，它是最大似然推理框架下的首选损失函数。它是首先评估的损失函数，只有在有充分理由的情况下才会更改。

交叉熵将计算一个分数，该分数汇总预测类别1的实际概率分布和预测概率分布之间的平均差异。该分数被最小化，完美的交叉熵值为0。

通过在编译模型时指定‘binary_crossentropy’，可以将交叉熵指定为Keras中的损失函数。

model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])

该函数要求输出层配置有单个节点和“sigmoid”激活，以便预测类别1的概率。

model.add(Dense(1, activation='sigmoid'))

下面列出了双圆二分分类问题的具有交叉熵损失的MLP的完整示例。

# mlp for the circles problem with cross entropy loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='sigmoid'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到模型很好地学习了问题，在训练数据集上达到了大约83%的准确率，在测试数据集上达到了大约85%的准确率。分数相当接近，这表明模型可能没有超过或不适合。

Train: 0.836, Test: 0.852

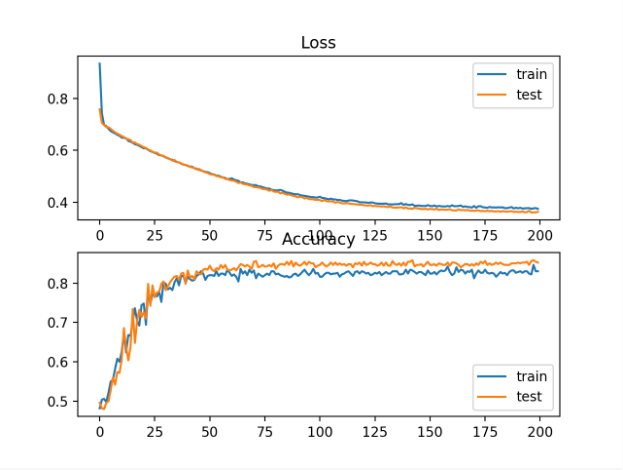
还创建了一个图，显示了两个线状图，顶部显示了训练(蓝色)和测试(橙色)数据集在epoch上的交叉熵损失，底部的曲线图显示了epoch上的分类精度。

结果表明，训练过程收敛良好。考虑到概率分布之间误差的连续性质，损失曲线图是平滑的，而精度曲线图显示凹凸不平，训练和测试集中的给定示例最终只能被预测为正确或不正确，从而提供较少粒度的性能反馈。

铰链损失

用于二元分类问题的交叉熵的另一种选择是铰链损失函数，该函数主要是为与支持向量机(SVM)模型一起使用而开发的。

它用于目标值在集合{-1，1}中的二进制分类。

铰链损耗函数鼓励示例具有正确的符号，当实际和预测的类值之间存在符号差异时，分配更多的误差。

关于铰链损失的性能报告喜忧参半，有时会导致在二进制分类问题上比交叉熵的性能更好。

首先，必须修改目标变量，使其具有集合{-1，1}中的值。

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

然后可以将铰链损失函数指定为编译函数中的‘hinge’。

model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])

最后，必须将网络的输出层配置为具有能够输出范围[-1，1]中的单个值的双曲正切激活函数的单个节点。

model.add(Dense(1, activation='tanh'))

下面列出了具有铰链损失函数的双圆二元分类问题的MLP的完整示例。

# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到性能略低于使用交叉熵，所选的模型配置在训练和测试集上的准确率低于80%。

Train: 0.792, Test: 0.740

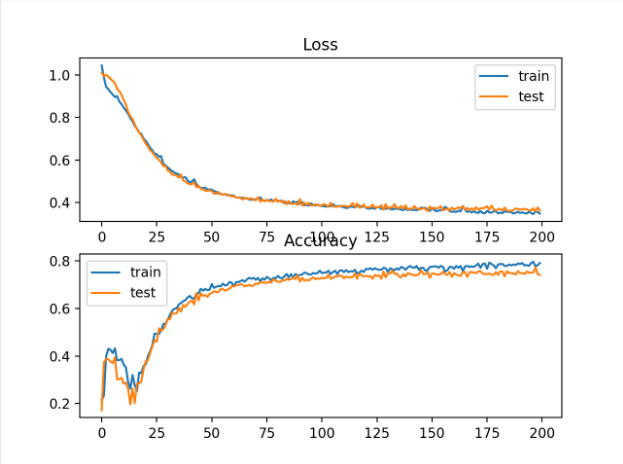
还创建了一个图形，显示了两个线状图，顶部显示了训练(蓝色)和测试(橙色)数据集在epoch上的铰链损耗，底部的曲线图显示了epoch上的分类精度。

铰链损失曲线图表明，模型已经收敛，在两个数据集上都有合理的损失。分类准确性的曲线图也显示出趋同的迹象，尽管在这个问题上的技能水平比人们所希望的要低。

平方铰链损失

铰链损失函数有许多扩展，通常是支持向量机模型研究的对象。

一个流行的扩展被称为铰链损失的平方，它简单地计算得分铰链损失的平方。它的作用是平滑误差函数的曲面，并使其在数值上更容易处理。

如果使用铰链损耗确实能在给定的二进制分类问题上产生更好的性能，则铰链损耗的平方可能是合适的。

与使用铰链损失函数一样，目标变量必须修改为具有集合{-1，1}中的值。

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

定义模型时，可以在compile()函数中将铰链损耗平方指定为‘squared_hinger’。

model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])

最后，输出层必须使用具有双曲正切激活函数的单节点，该节点能够输出范围[-1，1]内的连续值。

model.add(Dense(1, activation='tanh'))

下面列出了双圆二元分类问题上具有平方铰链损失函数的MLP的完整示例。

# mlp for the circles problem with squared hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到，对于这个问题和选择的模型配置，铰链平方损失可能是不合适的，导致在训练和测试集上的分类准确率低于70%。

Train: 0.682, Test: 0.646

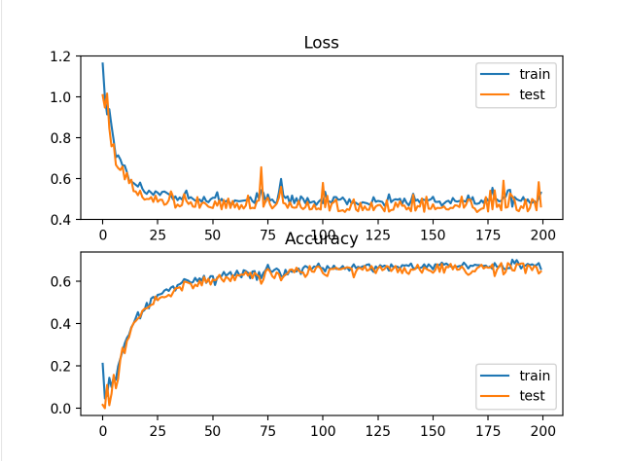
还创建了一个图，显示了两个线状图，上图显示了训练(蓝色)和测试(橙色)数据集在epoch上的平方铰链损耗，下图显示了epoch上的分类精度。

损失图显示，模型确实收敛了，但误差面的形状不像其他损失函数那样平滑，在其他损失函数中，权重的微小变化会导致损失的巨大变化。

多类分类损失函数

多类分类是那些预测建模问题，其中样本被分配到两个以上类别中的一个。

问题通常被框定为预测一个整数值，其中每个类都被分配了一个从0到(num_class-1)的唯一整数值。该问题通常被实现为预测示例属于每个已知类别的概率。

在本节中，我们将研究适用于多类分类预测建模问题的损失函数。

我们将以斑点问题作为调查的基础。scikit-learn提供的make_blobs()函数提供了一种在给定指定数量的类和输入特性的情况下生成示例的方法。我们将使用此函数为具有2个输入变量的3类分类问题生成1,000个示例。伪随机数生成器将被一致地设定种子，以便每次运行代码时生成相同的1,000个示例。

# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

这两个输入变量可以作为二维平面上的点的x和y坐标。

下面的示例按类成员身份创建整个数据集着色点的散点图。

# scatter plot of blobs dataset
from sklearn.datasets import make_blobs
from numpy import where
from matplotlib import pyplot
# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# select indices of points with each class label
for i in range(3):
	samples_ix = where(y == i)
	pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1])
pyplot.show()

运行该示例将创建一个散点图，显示数据集中的1,000个示例，其中的示例分别属于0、1和2类颜色蓝色、橙色和绿色。

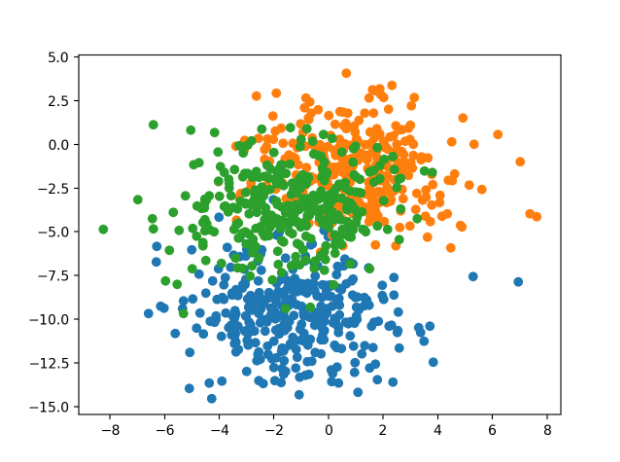
输入要素是高斯的，可以从标准化中获益；不过，为简洁起见，我们将保持本例中的值未缩放。

数据集将在训练集和测试集之间平均分割。

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

将使用一个小的MLP模型作为探索损失函数的基础。

该模型期望两个输入变量，隐含层和修正后的线性激活函数有50个节点，输出层必须根据损失函数的选择进行定制。

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(..., activation='...'))

模型采用随机梯度下降法拟合，合理的默认学习率为0.01，动量为0.9。

# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

该模型将适用于训练数据集上的100个epoch，测试数据集将用作验证数据集，使我们能够在每个训练epoch结束时评估训练集和测试集的损失和分类精度，并绘制学习曲线。

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

现在我们有了问题和模型的基础，我们可以看一看评估适用于多类分类预测建模问题的三个常见损失函数。

虽然在这些示例中使用了MLP，但是在训练用于多类分类的CNN和RNN模型时可以使用相同的损失函数。

多类交叉熵损失

交叉熵是用于多类分类问题的默认损失函数。

在这种情况下，它适用于目标值位于集合{0，1，3，…]中的多类分类。，n}，其中每个类都分配有唯一的整数值。

从数学上讲，它是最大似然推理框架下的首选损失函数。它是首先评估的损失函数，只有在有充分理由的情况下才会更改。

交叉熵将计算出一个分数，该分数汇总了问题中所有类别的实际概率分布和预测概率分布之间的平均差异。分数被最小化，并且完美的交叉熵值为0。

通过在编译模型时指定‘categorical_crossentropy’，可以将交叉熵指定为KERS中的损失函数。

model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

该功能要求输出层配置有n个节点(每个类别一个)，在这种情况下为三个节点，以及‘softmax’激活，以便预测每个类别的概率。

model.add(Dense(3, activation='softmax'))

反过来，这意味着目标变量必须是热编码的。

这是为了确保每个示例的实际类值的预期概率为1.0，所有其他类值的预期概率为0.0。这可以使用to_categorical() Keras函数来实现。

# one hot encode output variable
y = to_categorical(y)

下面列出了用于多类斑点分类问题的具有交叉熵损失的MLP的完整示例。

# mlp for the blobs multi-class classification problem with cross-entropy loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到该模型表现良好，在训练数据集上的分类准确率约为84%，在测试数据集上的分类准确率约为82%。

Train: 0.840, Test: 0.822

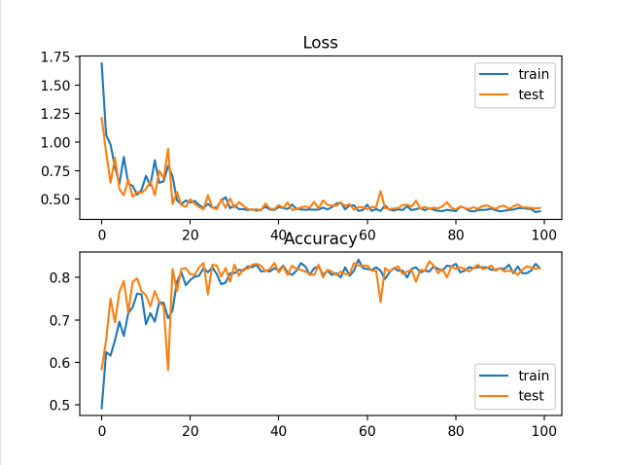
还创建了一个图，显示了两个线状图，顶部显示了训练(蓝色)和测试(橙色)数据集在epoch上的交叉熵损失，底部的曲线图显示了epoch上的分类精度。

在这种情况下，曲线图显示模型似乎已经收敛。交叉熵和精确度的直线图都表现出良好的收敛行为，尽管有些坎坷。如果没有过高或过低的迹象，模型可以配置得很好。在这种情况下，可以调整学习速率或批大小以均衡收敛的平滑度。

稀疏多类交叉熵损失

当使用具有大量标签的分类问题的交叉熵时，一个可能的挫败原因是一个热门的编码过程。

例如，预测词汇表中的单词可能有数万或数十万个类别，每个标签对应一个类别。这可能意味着每个训练示例的目标元素可能需要一个具有数万或数十万个零值的热编码向量，这需要大量的存储器。

稀疏交叉熵通过执行相同的误差交叉熵计算来解决这一问题，而不需要在训练之前对目标变量进行一个热编码。

通过在调用compile()函数时使用‘sparse_categorical_crossentropy’，可以在Keras中使用稀疏交叉熵进行多类分类。

model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

该功能要求输出层配置有n个节点(每个类别一个)，在这种情况下为三个节点，以及‘softmax’激活，以便预测每个类别的概率。

model.add(Dense(3, activation='softmax'))

不需要对目标变量进行任何热编码，这是此损失函数的好处。

下面列出了在斑点多类分类问题上训练具有稀疏交叉熵的MLP的完整示例。

# mlp for the blobs multi-class classification problem with sparse cross-entropy loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到该模型在该问题上取得了良好的性能。事实上，如果多次重复实验，稀疏和非稀疏交叉熵的平均性能应该是相当的。

Train: 0.832, Test: 0.818

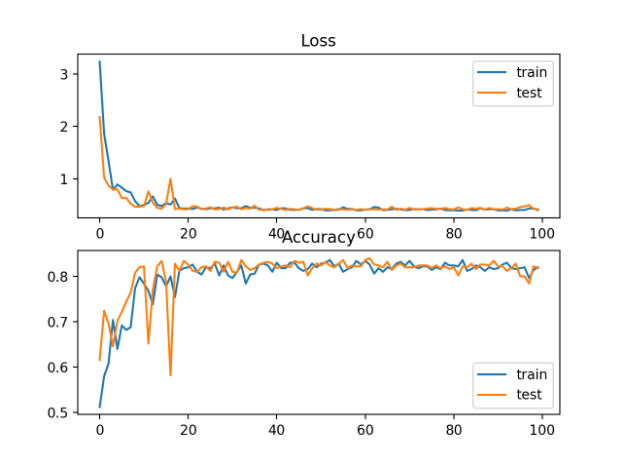
还创建了一个图，显示了两个线状图，上图显示了训练(蓝色)和测试(橙色)数据集在epoch上的稀疏交叉熵损失，下图显示了epoch上的分类精度。

在这种情况下，曲线图显示了模型在损失和分类精度方面优于训练的良好收敛性。

Kullback Leibler发散损失

Kullback Leibler发散，或简称KL发散，是衡量一个概率分布与基线分布有多大不同的一种度量。

KL发散损失为0表示分布是相同的。在实践中，KL发散的行为与交叉熵非常相似。如果预测的概率分布用于近似期望的目标概率分布，则它计算丢失多少信息(以比特为单位)。

因此，当使用学习近似比简单的多类分类更复杂的函数的模型时，例如在用于在必须重构原始输入的模型下学习密集特征表示的自动编码器的情况下，更常用KL发散损失函数。在这种情况下，最好采用KL发散损失。然而，它可以用于多类分类，在这种情况下，它在功能上等价于多类交叉熵。

KL发散损失可以在KERA中使用，方法是在compile()函数中指定‘kullback_leibler_divergence’。

model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])

与交叉熵一样，输出层被配置有n个节点(每个类别一个)，在这种情况下为三个节点，以及‘softmax’激活，以便预测每个类别的概率。

此外，与分类交叉熵一样，我们必须对目标变量进行热编码，使其类值的预期概率为1.0，所有其他类值的预期概率为0.0。

# one hot encode output variable
y = to_categorical(y)

下面列出了针对斑点多类分类问题训练具有KL发散损失的MLP的完整示例。

# mlp for the blobs multi-class classification problem with kl divergence loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# one hot encode output variable
y = to_categorical(y)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

运行该示例首先打印训练和测试数据集上模型的分类精度。

鉴于训练算法的随机性，你的具体结果可能会有所不同。尝试将该示例运行几次。

在这种情况下，我们看到的性能与交叉熵损失的结果相似，在这种情况下，在训练和测试数据集上的准确率约为82%。

Train: 0.822, Test: 0.822

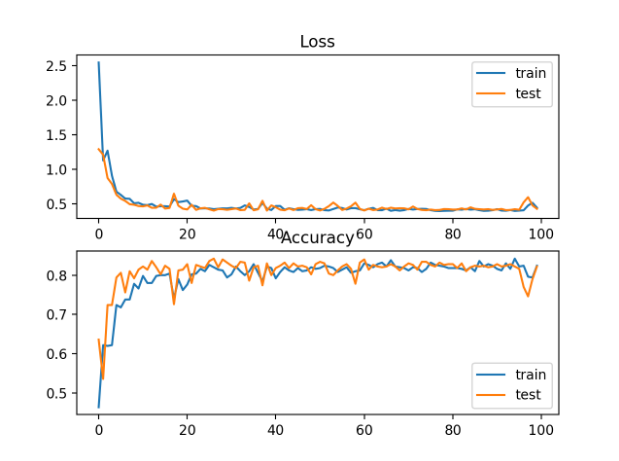
还创建了一个图，显示了两个线图，上图显示了训练(蓝色)和测试(橙色)数据集在epoch上的KL发散损失，下图显示了epoch上的分类精度。

在这种情况下，曲线图在损失和分类精度方面都表现出了良好的收敛行为。考虑到度量的相似性，交叉熵的评估很可能会导致几乎相同的行为。

进一步阅读

如果你想深入了解，本节提供了更多关于该主题的资源。

文章

• 用于训练深度学习神经网络的损失和损失函数。

论文

• 关于深度神经网络在分类中的损失函数，2017。

API接口

• Keras损失函数API。
• Keras激活函数API。
• sklearn.preprocessing.StandardScaler API。
• sklearn.datets.make_regations API。
• sklearn.datets.make_circles API。
• sklearn.datets.make_blobs API。

文章

• 均方误差，维基百科。
• 平均绝对误差，维基百科。
• 交叉熵，维基百科。
• 铰链损失，维基百科。
• Kullback Leibler发散，维基百科。
• 神经网络中的损失函数，2017。

摘要

在本教程中，你了解了如何为给定预测建模问题的深度学习神经网络选择损失函数。

具体地说，你了解到：

• 如何为回归问题配置均方误差和变量模型。
• 如何为二进制分类配置交叉熵和铰链损失函数的模型。
• 如何为多类分类配置交叉熵和KL发散损失函数的模型。

10

Python