如何用节点和层控制神经网络模型容量

0
2020-05-24
机器学习
0
0

深度学习神经网络模型的能力控制其能够学习的映射函数类型的范围。

容量太小的模型无法学习训练数据集，这意味着它将不适合，而容量太大的模型可能会记忆训练数据集，这意味着它将过度适应，或者可能在优化过程中卡住或丢失。

通过配置节点数和层数来定义神经网络模型的容量。

在本教程中，你将了解如何控制神经网络模型的容量，以及容量如何影响模型的学习能力。

完成本教程后，你将了解：

神经网络模型的容量由模型中的节点数和层数共同控制。
具有单个隐含层和足够数量的节点的模型具有学习任何映射函数的能力，但是所选择的学习算法可能能够也可能不能够实现这一能力。
增加层数提供了用更少的资源增加模型容量的捷径，现代技术允许学习算法成功地训练深度模型。

我们开始吧。

教程概述

本教程分为五个部分；它们是：

控制神经网络模型容量。
在Keras中配置节点和图层。
多类分类问题。
使用节点更改模型容量。
使用图层更改模型容量。

控制神经网络模型容量

神经网络的目标是学习如何将输入示例映射到输出示例。

神经网络学习映射函数。网络容量指的是模型可以近似的功能类型的范围或范围。

非正式地说，模型的能力就是它适应各种功能的能力。

容量较小的模型可能不能充分学习训练数据集。具有更大容量的模型可以对更多不同类型的函数建模，并且可能能够学习函数以将输入充分映射到训练数据集中的输出。而容量过大的模型可能会记住训练数据集，并且在搜索合适的映射函数时可能无法概括或迷路或陷入困境。

通常，我们可以将模型容量视为对模型是否可能不适合或过适合训练数据集的控制。

我们可以通过改变一个模型的容量来控制它是更有可能过大还是不合适。

神经网络的容量可以由模型的两个方面控制：

节点数。
层数。

具有更多节点或更多层的模型具有更大的容量，进而潜在地能够学习更大的映射函数集。

具有更多层和每层更多隐藏单元的模型具有更高的表示能力-它能够表示更复杂的功能。

层中的节点数称为宽度。

开发具有一层和多个节点的宽广网络相对简单。理论上，单个隐层有足够节点的网络可以学习逼近任何映射函数，但在实践中，我们不知道有多少个节点就足够了，也不知道如何训练这样的模型。

模型中的层数称为其深度。

增加深度会增加模型的容量。与训练具有大量节点的单层网络相比，训练深度模型(例如，具有许多隐藏层的模型)在计算上可以更有效。

现代深度学习为监督学习提供了一个非常强大的框架。通过添加更多层和层内的更多单元，深层网络可以表示日益复杂的功能。

传统上，由于梯度消失等问题，训练多层神经网络模型一直具有挑战性。最近，现代方法使得深层网络模型的训练成为可能，使得能够开发出具有惊人深度的模型，这些模型能够在广泛领域的挑战性问题上取得令人印象深刻的性能。

在Keras中配置节点和图层

Keras允许你轻松地向模型添加节点和层。

配置模型节点

层的第一个参数指定层中使用的节点数。

多层感知器(MLP)模型的完全连接层是通过致密层添加的。

例如，我们可以创建一个具有32个节点的完全连接层，如下所示：

...
layer = Dense(32)

类似地，可以以相同的方式指定递归神经网络层的节点数。

例如，我们可以创建一个包含32个节点(或单元)的LSTM层，如下所示：

...
layer = LSTM(32)

卷积神经网络，或CNN，没有节点，而是指定过滤器映射的数量和它们的形状。过滤器贴图的数量和大小定义了层的容量。

我们可以定义一个具有32个滤波图的二维CNN，每个滤波图的大小为3乘3，如下所示：

...
layer = Conv2D(32, (3,3))

配置模型层

通过调用add()函数并传入层，将层添加到顺序模型中。

可以通过重复调用来添加MLP的完全连接层，以添加配置的密集层中的传递；例如：

...
model = Sequential()
model.add(Dense(32))
model.add(Dense(64))

类似地，递归网络的层数可以以相同的方式添加，以给出堆叠递归模型。

一个重要的区别是，递归层期望三维输入，因此前一个递归层必须返回完整的输出序列，而不是输入序列末尾的每个节点的单个输出。

这可以通过将“return_sequences”参数设置为“True”来实现。例如：

...
model = Sequential()
model.add(LSTM(32, return_sequences=True))
model.add(LSTM(32))

卷积层可以直接堆叠，通常将一个或两个卷积层堆叠在一起，然后是一个池化层，然后重复此层模式；例如：

...
model = Sequential()
model.add(Conv2D(16, (3,3)))
model.add(Conv2D(16, (3,3)))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(32, (3,3)))
model.add(Conv2D(32, (3,3)))
model.add(MaxPooling2D((2,2)))

现在我们已经了解了如何在Keras中配置模型的节点和层的数量，我们可以看看容量如何影响多类分类问题上的模型性能。

多类分类问题

我们将使用一个标准的多类分类问题作为基础来演示模型容量对模型性能的影响。

scikit-learn类提供make_blobs()函数，该函数可用于创建具有指定数量的样本、输入变量、类和类中样本的方差的多类分类问题。

我们可以通过“n_features”参数将问题配置为具有特定数量的输入变量，并通过“centers”参数将问题配置为具有特定数量的类或中心。“random_state”可用于设定伪随机数生成器的种子，以确保每次调用函数时始终获得相同的样本。

例如，下面的调用为具有两个输入变量的三类问题生成1000个示例。

...
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

结果是我们可以建模的数据集的输入和输出元素。

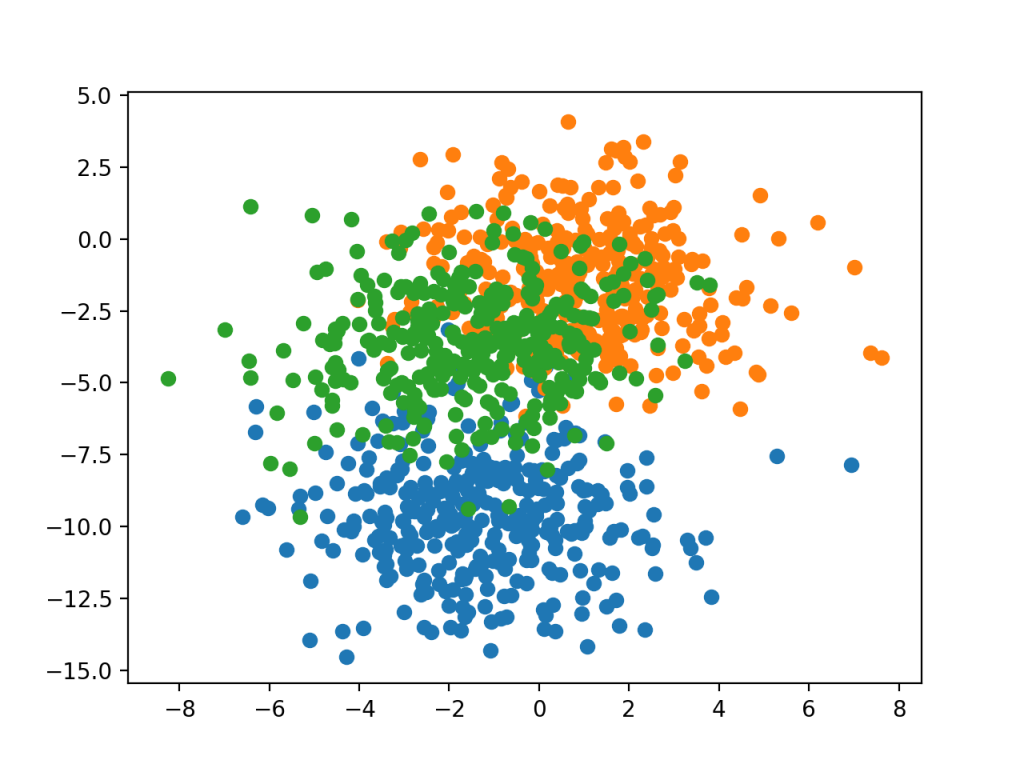
为了了解问题的复杂性，我们可以在二维散点图上绘制每个点，并按类值对每个点进行着色。

下面列出了完整的示例。

# scatter plot of blobs dataset
from sklearn.datasets import make_blobs
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# scatter plot for each class value
for class_value in range(3):
	# select indices of points with the class label
	row_ix = where(y == class_value)
	# scatter plot for points with a different color
	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# show plot
pyplot.show()

运行该示例将创建整个数据集的散点图。我们可以看到，选择的标准偏差2.0意味着类不是线性可分的(可以用一条线分开)，这会导致很多模糊点。

这是可取的，因为它意味着问题不是微不足道的，并将允许神经网络模型找到许多不同的“足够好”的候选解决方案。

为了探索模型的容量，我们需要比三类两变量更复杂的问题。

出于以下实验的目的，我们将使用100个输入要素和20个类；例如：

...
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2)

使用节点更改模型容量

在本节中，我们将为斑点多类分类问题开发一个多层感知器模型(MLP)，并演示节点数量对模型学习能力的影响。

我们可以从开发一个函数来准备数据集开始。

如上一节所述，可以使用make_blobs()函数创建数据集的输入和输出元素。

接下来，目标变量必须是一个热编码变量。这使得模型可以学习预测属于20个类别中的每个类别的输入示例的概率。

我们可以使用to_categorical()Keras实用函数来执行此操作，例如：

# one hot encode output variable
y = to_categorical(y)

接下来，我们可以将1000个样本一分为二，并使用500个样本作为训练数据集，500个样本来评估模型。

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
return trainX, trainy, testX, testy

下面的create_dataset()函数将这些元素绑定在一起，并根据输入和输出元素返回训练和测试集。

# prepare multi-class classification dataset
def create_dataset():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

我们可以调用此函数来准备数据集。

# prepare dataset
trainX, trainy, testX, testy = create_dataset()

接下来，我们可以定义一个函数来创建模型，使其适合训练数据集，然后在测试数据集上对其进行评估。

模型需要知道输入变量的数量才能配置输入层，也需要知道目标类的数量才能配置输出层。这些属性可以直接从训练数据集中提取。

# configure the model based on the data
n_input, n_classes = trainX.shape[1], testy.shape[1]

我们将定义一个具有单个隐层的MLP模型，该模型使用校正的线性激活函数和随机权重初始化方法。

输出层将使用softmax 激活函数来预测每个目标类的概率。隐藏层中的节点数将通过名为“n_nodes”的参数提供。

# define model
model = Sequential()
model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(n_classes, activation='softmax'))

模型将采用随机梯度下降进行优化，适度学习率为0.01，高动量为0.9，并采用分类交叉熵损失函数，适用于多类分类。

# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

该模型将适用于100个训练周期，然后在测试数据集上对该模型进行评估。

# fit model on train set
history = model.fit(trainX, trainy, epochs=100, verbose=0)
# evaluate model on test set
_, test_acc = model.evaluate(testX, testy, verbose=0)

将这些元素捆绑在一起，下面的evaluate_model()函数将节点和数据集的数量作为参数，并返回每个时段结束时训练损失的历史记录以及测试数据集上最终模型的精度。

# fit model with given number of nodes, returns test set accuracy
def evaluate_model(n_nodes, trainX, trainy, testX, testy):
	# configure the model based on the data
	n_input, n_classes = trainX.shape[1], testy.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(n_classes, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=0.9)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model on train set
	history = model.fit(trainX, trainy, epochs=100, verbose=0)
	# evaluate model on test set
	_, test_acc = model.evaluate(testX, testy, verbose=0)
	return history, test_acc

我们可以在隐藏层中使用不同数量的节点来调用此函数。

问题相对简单；因此，我们将回顾具有1到7个节点的模型的性能。

我们预计，随着节点数量的增加，这将增加模型的容量，并允许模型更好地学习训练数据集，至少达到受学习算法的所选配置(例如，学习速率、批大小和历元)限制的点。

将打印每个配置的测试精度，并绘制每个配置的训练精度学习曲线。

# evaluate model and plot learning curve with given number of nodes
num_nodes = [1, 2, 3, 4, 5, 6, 7]
for n_nodes in num_nodes:
	# evaluate model with a given number of nodes
	history, result = evaluate_model(n_nodes, trainX, trainy, testX, testy)
	# summarize final test set accuracy
	print('nodes=%d: %.3f' % (n_nodes, result))
	# plot learning curve
	pyplot.plot(history.history['loss'], label=str(n_nodes))
# show the plot
pyplot.legend()
pyplot.show()

为了完整起见，下面提供了完整的代码清单。

# study of mlp learning curves given different number of nodes for multi-class classification
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot

# prepare multi-class classification dataset
def create_dataset():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit model with given number of nodes, returns test set accuracy
def evaluate_model(n_nodes, trainX, trainy, testX, testy):
	# configure the model based on the data
	n_input, n_classes = trainX.shape[1], testy.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(n_classes, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=0.9)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model on train set
	history = model.fit(trainX, trainy, epochs=100, verbose=0)
	# evaluate model on test set
	_, test_acc = model.evaluate(testX, testy, verbose=0)
	return history, test_acc

# prepare dataset
trainX, trainy, testX, testy = create_dataset()
# evaluate model and plot learning curve with given number of nodes
num_nodes = [1, 2, 3, 4, 5, 6, 7]
for n_nodes in num_nodes:
	# evaluate model with a given number of nodes
	history, result = evaluate_model(n_nodes, trainX, trainy, testX, testy)
	# summarize final test set accuracy
	print('nodes=%d: %.3f' % (n_nodes, result))
	# plot learning curve
	pyplot.plot(history.history['loss'], label=str(n_nodes))
# show the plot
pyplot.legend()
pyplot.show()

运行该示例首先打印每个型号配置的测试精度。

由于学习算法的随机性，你的具体结果会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到，随着节点数量的增加，模型学习问题的能力也随之增加。这导致模型在测试数据集上的泛化误差逐渐降低，直到模型完全学习问题时的6个和7个节点。

nodes=1: 0.138
nodes=2: 0.380
nodes=3: 0.582
nodes=4: 0.890
nodes=5: 0.844
nodes=6: 1.000
nodes=7: 1.000

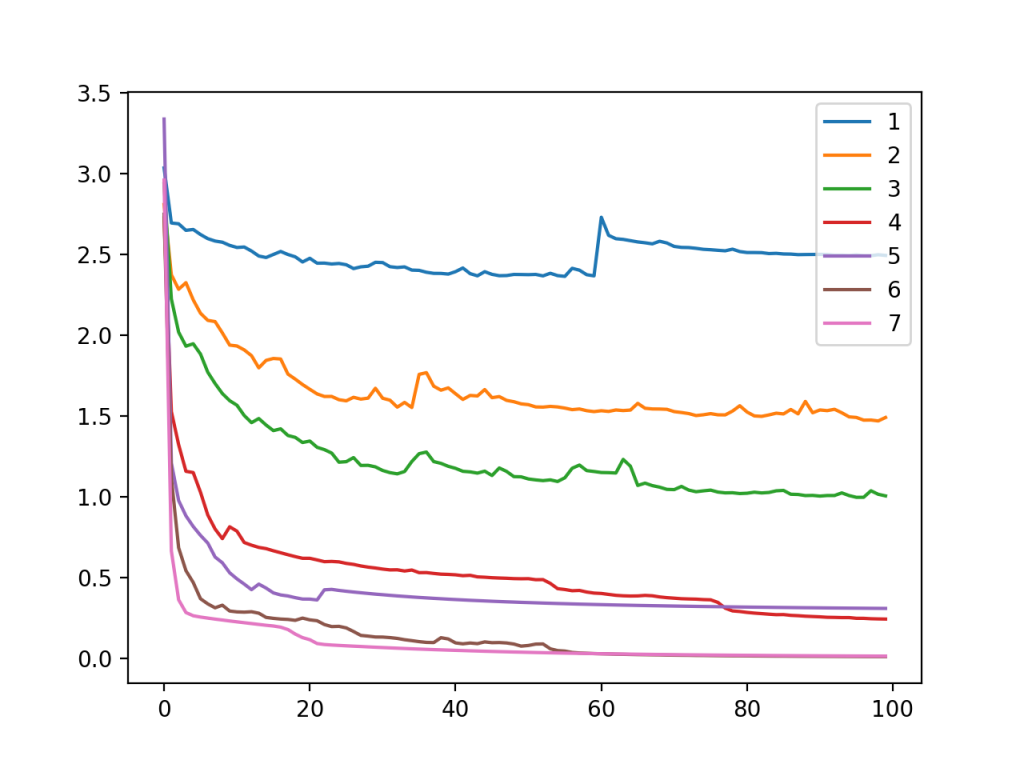
还创建了显示100个训练时段上每个模型配置(隐藏层中的1到7个节点)的训练数据集上的交叉熵损失的线图。

我们可以看到，随着节点数量的增加，模型能够更好地减少损失，例如更好地学习训练数据集。此图显示了模型容量(由隐藏层中的节点数定义)与模型的学习能力之间的直接关系。

节点的数量可以增加到学习算法不再能够充分学习映射函数的点(例如，1000个节点)。

使用图层更改模型容量

我们可以执行类似的分析，并评估层的数量如何影响模型学习映射函数的能力。

增加层数通常可以极大地增加模型的容量，就像是为问题建模的计算和学习捷径。例如，具有10个节点的一个隐藏层的模型不等同于具有两个隐藏层的模型，每个隐藏层具有5个节点。后者的容量要大得多。

危险在于，具有比所需容量更大的容量的模型可能会过度拟合训练数据，并且与具有太多节点的模型一样，具有太多层的模型可能无法学习训练数据集，从而在优化过程中迷路或卡住。

首先，我们可以更新EVALUATE_MODEL()函数，使其适合具有给定层数的MLP模型。

我们从上一节了解到，具有大约七个或更多节点的MLP适合100个历元，将完美地学习该问题。因此，我们将在每层中使用10个节点，以确保模型仅在一层中就有足够的容量来学习问题。

下面列出了更新后的函数，它以层数和数据集为参数，并返回模型的训练历史和测试精度。

# fit model with given number of layers, returns test set accuracy
def evaluate_model(n_layers, trainX, trainy, testX, testy):
	# configure the model based on the data
	n_input, n_classes = trainX.shape[1], testy.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(10, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
	for _ in range(1, n_layers):
		model.add(Dense(10, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(n_classes, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=0.9)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, epochs=100, verbose=0)
	# evaluate model on test set
	_, test_acc = model.evaluate(testX, testy, verbose=0)
	return history, test_acc

考虑到单个隐层模型有足够的能力学习这个问题，我们将探索增加层数到学习算法变得不稳定并且不能再学习问题的程度。

如果选择的建模问题更复杂，我们可以探索增加层，并审查模型性能的改进，使其达到回报递减的程度。

在这种情况下，我们将用1到5层来评估模型，期望在某个点上，层的数量会导致所选择的学习算法无法适应训练数据的模型。

# evaluate model and plot learning curve of model with given number of layers
all_history = list()
num_layers = [1, 2, 3, 4, 5]
for n_layers in num_layers:
	# evaluate model with a given number of layers
	history, result = evaluate_model(n_layers, trainX, trainy, testX, testy)
	print('layers=%d: %.3f' % (n_layers, result))
	# plot learning curve
	pyplot.plot(history.history['loss'], label=str(n_layers))
pyplot.legend()
pyplot.show()

将这些元素捆绑在一起，完整的示例如下所示。

# study of mlp learning curves given different number of layers for multi-class classification
from sklearn.datasets import make_blobs
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot

# prepare multi-class classification dataset
def create_dataset():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit model with given number of layers, returns test set accuracy
def evaluate_model(n_layers, trainX, trainy, testX, testy):
	# configure the model based on the data
	n_input, n_classes = trainX.shape[1], testy.shape[1]
	# define model
	model = Sequential()
	model.add(Dense(10, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
	for _ in range(1, n_layers):
		model.add(Dense(10, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(n_classes, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=0.9)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, epochs=100, verbose=0)
	# evaluate model on test set
	_, test_acc = model.evaluate(testX, testy, verbose=0)
	return history, test_acc

# get dataset
trainX, trainy, testX, testy = create_dataset()
# evaluate model and plot learning curve of model with given number of layers
all_history = list()
num_layers = [1, 2, 3, 4, 5]
for n_layers in num_layers:
	# evaluate model with a given number of layers
	history, result = evaluate_model(n_layers, trainX, trainy, testX, testy)
	print('layers=%d: %.3f' % (n_layers, result))
	# plot learning curve
	pyplot.plot(history.history['loss'], label=str(n_layers))
pyplot.legend()
pyplot.show()

运行该示例首先打印每个型号配置的测试精度。

由于学习算法的随机性，你的具体结果会有所不同。尝试将该示例运行几次。

在这种情况下，我们可以看到模型能够在最多三层的情况下很好地学习问题，然后开始步履蹒跚。我们可以看到，性能真的下降了五层，如果层数进一步增加，预计还会继续下降。

layers=1: 1.000
layers=2: 1.000
layers=3: 1.000
layers=4: 0.948
layers=5: 0.794

还创建了显示100个训练时段内每个模型配置(1到5层)的训练数据集上的交叉熵损失的线图。

我们可以看到，具有1、2和3个模型(蓝色、橙色和绿色)的模型的动力学非常相似，学习问题的速度很快。

令人惊讶的是，具有四层和五层的训练损失显示出最初表现良好的迹象，然后跃升，这表明模型可能停留在次优的权重集上，而不是过度拟合训练数据集。

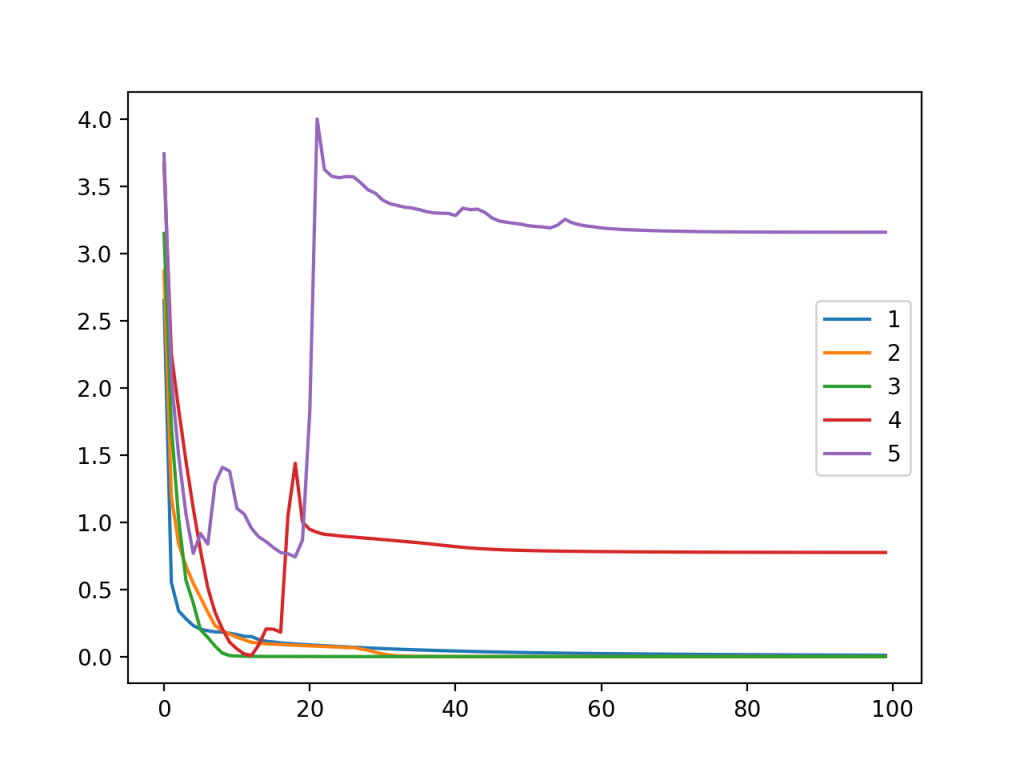
分析表明，通过增加深度来增加模型的容量是一个非常有效的工具，必须谨慎使用，因为它很快就会导致一个容量很大的模型，而这个模型可能不容易学习训练数据集。

拓展

本节列出了一些你可能希望了解的扩展教程的想法。

节点太多。更新增加节点的实验，找到学习算法不再能够学习问题的点。
重复评估。更新实验以使用每个配置的重复评估来对抗学习算法的随机性。
更难的问题。对于一个问题重复增加层的实验，该问题需要通过增加深度提供更大的容量才能很好地执行。

进一步阅读

如果你想深入了解，本节提供了更多关于该主题的资源。

文章

如何配置神经网络中的层数和节点数。

书籍

API接口

文章

我应该使用多少个隐藏层？，comp.ai.neural-nets 常见问题解答

摘要

在本教程中，你了解了如何控制神经网络模型的容量，以及容量如何影响模型的学习能力。

具体地说，你了解到：

神经网络模型的容量由模型中的节点数和层数共同控制。
具有单个隐层和足够数量的节点的模型具有学习任何映射函数的能力，但是所选择的学习算法可能能够也可能不能够实现这一能力。
增加层数提供了用更少的资源增加模型容量的捷径，现代技术允许学习算法成功地训练深度模型。

0 0

Python

如何用节点和层控制神经网络模型容量

教程概述

控制神经网络模型容量

在Keras中配置节点和图层

配置模型节点

配置模型层

多类分类问题

使用节点更改模型容量

使用图层更改模型容量

拓展

进一步阅读

文章

书籍

API接口

文章

摘要

发表评论取消回复

什么阻碍了你实现迈入机器学习领域的目标？

R语言机器学习迷你课程

关于机器学习的几点思考

找到你的机器学习部落

应用机器学习过程

你或许会喜欢