校正线性单元(ReLU)介绍

0
2020-05-10
机器学习
0
0

在神经网络中，激活函数负责将来自节点的总和加权输入转换为该输入的节点或输出的激活。

校正后的线性激活函数是分段线性函数，如果为正则直接输出输入，否则输出零。它已经成为许多类型神经网络的默认激活函数，因为使用它的模型更容易训练，并且通常获得更好的性能。

在本教程中，您将发现深度学习神经网络的校正线性激活函数。

完成本教程后，您将了解：

由于梯度消失问题，Sigmoid和双曲正切激活函数不能用于多层网络。
修正后的线性激活函数克服了梯度消失的问题，使模型学习速度更快，性能更好。
在开发多层感知器和卷积神经网络时，整流线性激活是默认的激活。

我们开始吧。

教程概述

本教程分为六个部分，它们是：

Sigmoid和Tanh激活函数的局限性。
修正的线性激活函数。
如何实现整流线性激活功能。
整流型线性激励器的优点。
使用整流线性激活器的技巧。
ReLU的扩展和替代方案。

Sigmoid和Tanh激活函数的局限性

神经网络由节点层组成，学习将输入示例映射到输出。

对于给定节点，输入乘以节点中的权重，然后相加在一起。该值称为节点的总和激活。然后，通过激活函数对总和激活进行转换，并定义节点的特定输出或“激活”。

最简单的激活函数称为线性激活，其中根本不应用任何变换。仅由线性激活函数组成的网络非常容易训练，但不能学习复杂的映射函数。线性激活函数仍然用于预测量(例如回归问题)的网络的输出层。

非线性激活函数是优选的，因为它们允许节点学习数据中更复杂的结构。传统上，两种广泛使用的非线性激活函数是Sigmoid和双曲正切激活函数。

Sigmoid激活函数，也称为Logistic函数，传统上是一种非常流行的神经网络激活函数。函数的输入转换为0.0到1.0之间的值。大于1.0的输入将变换为值1.0，同样，小于0.0的值将捕捉到0.0。对于所有可能的输入，函数的形状是从零到0.5到1.0的S形。在很长一段时间里，直到20世纪90年代初，它都是神经网络使用的默认激活。

双曲正切函数，或简称为tanh，是一个类似形状的非线性激活函数，其输出值介于-1.0和1.0之间。在20世纪90年代后期和21世纪头10年，TanH函数比Sigmoid激活函数更受欢迎，因为使用它的模型更容易训练，而且通常具有更好的预测性能。

……双曲正切激活函数通常比逻辑Sigmoid表现得更好。

Sigmoid函数和tanh函数的一个普遍问题是它们饱和了。这意味着对于tanh和sigmoid，大值捕捉到1.0，小值捕捉到-1或0。此外，这些函数只对其输入中点附近的变化非常敏感，例如，Sigmoid为0.5，tanh为0.0。

无论来自作为输入提供的节点的总和激活是否包含有用信息，都会发生功能的有限灵敏度和饱和度。一旦达到饱和，对于学习算法来说，继续调整权值以提高模型的性能就变得具有挑战性。

……S型单位在它们的大部分域上饱和-当z非常正时，它们饱和到一个高值，当z非常负时，它们饱和到一个低值，并且只有当z接近0时，它们才对它们的输入非常敏感。

最后，随着硬件能力的提高，使用Sigmoid和tanh激活函数的GPU的非常深的神经网络不容易训练。

使用这些非线性激活函数的大型网络深处的层不能接收有用的梯度信息。错误通过网络反向传播并用于更新权重。在给定所选激活函数的导数的情况下，误差量随着其传播通过的每一附加层而显著减小。这就是所谓的消失梯度问题，它阻碍了深层(多层)网络的有效学习。

渐变消失使得很难知道参数应该朝哪个方向移动以改进成本函数。

有关ReLU如何修复消失渐变问题的示例，请参见教程：

如何使用校正后的线性激活函数修正消失梯度。

虽然非线性激活函数的使用允许神经网络学习复杂的映射函数，但它们有效地阻止了学习算法与深度网络的结合。

在2000年代末和2010年代初，使用替代网络类型(如Boltzmann机器和分层训练或无人监督的预训练)找到了解决办法。

修正的线性激活函数

为了使用具有误差反向传播的随机梯度下降来训练深度神经网络，需要激活函数，该激活函数看起来和行为类似于线性函数，但实际上是允许学习数据中的复杂关系的非线性函数。

该功能还必须对激活和输入提供更高的灵敏度，并避免容易饱和。

这个解决方案在这个领域已经有一段时间了，尽管直到2009年和2011年的报纸对其进行了报道，这个解决方案才得到重视。

解决方案是使用校正的线性激活函数，或简称ReL。

实现该激活功能的节点或单元被称为校正线性激活单元，或简称为ReLU。通常，将整流器功能用于隐藏层的网络称为整流网络。

ReLU的采用可以很容易地被认为是深度学习革命中为数不多的里程碑之一，例如，现在允许常规开发非常深的神经网络的技术。

[另一个]极大地改善了前馈网络性能的主要算法改变是用分段线性隐藏单元(例如校正的线性单元)替换了S形隐藏单元。

校正后的线性激活函数是一个简单的计算，它直接返回作为输入提供的值，如果输入为0.0或更小，则返回值0.0。

我们可以用一个简单的if语句来描述这一点：

if input > 0:
	return input
else:
	return 0

我们可以在0.0的集合和输入z上使用max()函数以数学方式描述此函数g()；例如：

g(z) = max{0, z}

该函数对于大于零的值是线性的，这意味着当使用反向传播训练神经网络时，它具有线性激活函数的许多所需属性。然而，它是一个非线性函数，因为负值总是输出为零。

由于校正后的线性单位几乎是线性的，因此它们保留了许多属性，这些属性使得线性模型易于使用基于梯度的方法进行优化。它们还保留了使线性模型很好地泛化的许多属性。

因为校正后的函数对于输入域的一半是线性的，而对于另一半是非线性的，所以它被称为分段线性函数或铰链函数。

然而，从这个意义上说，该函数仍然非常接近线性，即具有两个线性段的分段线性函数。

现在我们已经熟悉了修正后的线性激活函数，让我们看看如何在Python中实现它。

如何对校正后的线性激活函数进行编码

我们可以很容易地在Python中实现校正后的线性激活函数。

也许最简单的实现是使用max()函数；例如：

# rectified linear function
def rectified(x):
	return max(0.0, x)

我们预计任何正值都将不变地返回，而输入值0.0或负值将作为值0.0返回。

下面是几个整流线性激活函数的输入和输出示例。

# demonstrate the rectified linear function

# rectified linear function
def rectified(x):
	return max(0.0, x)

# demonstrate with a positive input
x = 1.0
print('rectified(%.1f) is %.1f' % (x, rectified(x)))
x = 1000.0
print('rectified(%.1f) is %.1f' % (x, rectified(x)))
# demonstrate with a zero input
x = 0.0
print('rectified(%.1f) is %.1f' % (x, rectified(x)))
# demonstrate with a negative input
x = -1.0
print('rectified(%.1f) is %.1f' % (x, rectified(x)))
x = -1000.0
print('rectified(%.1f) is %.1f' % (x, rectified(x)))

运行该示例，我们可以看到，无论其大小如何，都会返回正值，而负值则捕捉到值0.0。

rectified(1.0) is 1.0
rectified(1000.0) is 1000.0
rectified(0.0) is 0.0
rectified(-1.0) is 0.0
rectified(-1000.0) is 0.0

我们可以通过绘制一系列的输入和计算的输出来了解函数的输入和输出之间的关系。

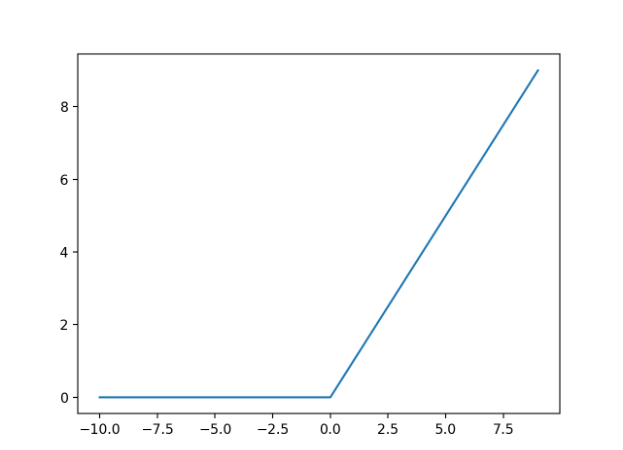
下面的示例生成从-10到10的一系列整数，并计算每个输入的校正线性激活，然后绘制结果。

# plot inputs and outputs
from matplotlib import pyplot

# rectified linear function
def rectified(x):
	return max(0.0, x)

# define a series of inputs
series_in = [x for x in range(-10, 11)]
# calculate outputs for our inputs
series_out = [rectified(x) for x in series_in]
# line plot of raw inputs to rectified outputs
pyplot.plot(series_in, series_out)
pyplot.show()

运行该示例将创建一个线形图，显示所有负值和零输入捕捉到0.0，而正输出按原样返回，从而导致线性递增的斜率，假设我们创建了一系列线性递增的正值(例如，1到10)。

修正后的线性函数的导数也很容易计算。回想一下，当作为误差反向传播的一部分更新节点的权重时，需要激活函数的导数。

函数的导数是斜率。负值的坡度为0.0，正值的坡度为1.0。

传统上，神经网络领域避免了任何不完全可微的激活函数，可能会延迟采用校正后的线性函数和其他分段线性函数。从技术上讲，当输入为0.0时，我们不能计算导数，因此，我们可以假设它是零。这在实践中不是问题。

例如，校正后的线性函数g(z) = max{0, z}在z=0处是不可微的。这看起来似乎使g无效，无法与基于梯度的学习算法一起使用。在实践中，梯度下降的性能仍然足够好，可以将这些模型用于机器学习任务。

使用校正后的线性激活函数有很多优点；让我们在下一节中看看其中几个。

整流线性激活函数的优点

在开发大多数类型的神经网络时，校正后的线性激活函数已迅速成为默认的激活函数。

因此，花点时间回顾一下该方法的一些好处是很重要的，Xavier Glorot等人首先强调了这一点。在2012年他们关于使用ReLU的里程碑式论文“深度稀疏整流器神经网络”中。

1.计算简单

整流器函数实现起来很简单，需要一个max()函数。

这与需要使用指数计算的tanh和sigmoid激活函数不同。

计算也更便宜：在激活时不需要计算指数函数。

2.表征稀疏性

整流器功能的一个重要优点是它能够输出真零值。

这不同于学习近似零输出的tanh和sigmoid激活函数，例如非常接近于零的值，但不是真正的零值。

这意味着负输入可以输出真零值，从而允许激活神经网络中的隐藏层以包含一个或多个真零值。这被称为稀疏表示，这是表象学习中的一个理想属性，因为它可以加速学习并简化模型。

研究和寻找诸如稀疏性之类的有效表示的领域是在自动编码器中，其中网络在从紧凑表示中重构输入(称为代码层)之前学习输入的紧凑表示(称为代码层)，例如图像或序列。

实现稀疏(和去噪)自动编码器h中实际零的一种方法……其思想是使用校正后的线性单元来产生码层。利用实际将表示推至零的先验(如绝对值惩罚)，因此可以间接控制表示中的平均零数。

3.线性行为

整流器功能主要看起来和行为类似于线性激活功能。

一般来说，当神经网络的行为是线性或接近线性时，它更容易优化。

校正的线性单位[…]是基于这样的原则，即如果模型的行为更接近于线性，则模型更容易优化。

这一特性的关键在于，用该激活函数训练的网络几乎完全避免了梯度消失的问题，因为梯度保持与节点激活成正比。

由于这种线性，梯度很好地在神经元的活动路径上流动(不存在由于S型或TANH单位的激活非线性而产生的梯度消失效应)。

4.训练深度网络

重要的是，(重新)发现和采用校正的线性激活函数意味着可以利用硬件的改进，并使用反向传播成功地训练具有非线性激活函数的深层多层网络。

反过来，像Boltzmann机器这样的繁琐网络可能会被抛在脑后，而像分层训练和无标签预训练这样的繁琐训练方案也可能被抛在脑后。

……深度整流网络可以达到其最佳性能，而不需要对具有大标签数据集的纯监督任务进行任何无监督的预训练。因此，这些结果可以被视为理解深度但纯监督神经网络训练难度的新里程碑，并缩小在无监督预训练和无监督预训练情况下学习的神经网络之间的性能差距。

使用整流线性激活器的技巧

在这一节中，我们将看看在您自己的深度学习神经网络中使用校正的线性激活函数时的一些提示。

使用ReLU作为默认激活功能

在很长一段时间内，使用的默认激活功能是乙状结肠激活功能。后来，它是TANH激活功能。

对于现代深度学习神经网络，缺省激活函数是修正后的线性激活函数。

在引入校正后的线性单元之前，大多数神经网络采用Logistic Sigmoid激活函数或双曲正切激活函数。

大多数获得最先进成果的论文都会描述使用RELU的网络。例如，在Alex Krizhevsky等人于2012年发表的里程碑式的论文中。题为“基于深度卷积神经网络的ImageNet分类”，作者开发了一种具有RELU激活的深度卷积神经网络，在ImageNet照片分类数据集上取得了最先进的结果。

……我们将具有这种非线性的神经元称为整流线性单位(RELU)。具有RELU的深度卷积神经网络的训练速度比具有TANH单元的等价物快数倍。

如果有疑问，可以从神经网络中的RELU开始，然后尝试其他分段线性激活函数，看看它们的性能如何比较。

在现代神经网络中，默认建议使用校正后的线性单位或ReLU。

将ReLU与MLP、CNN配合使用，但可能不与RNN配合使用。

ReLU可以与大多数类型的神经网络一起使用。

建议将其作为多层感知器(MLP)和卷积神经网络(CNN)的默认设置。

ReLU与CNN的使用已经被彻底调查，几乎普遍的结果是结果的改善，最初，令人惊讶的是这样。

……跟随滤波器组的非线性对识别精度有何影响？令人惊讶的答案是，使用校正非线性是提高识别系统性能的最重要的单一因素。

研究使用CNN的ReLU的工作正是促使它们与其他网络类型一起使用的原因。

[其他人]探索了各种校正后的非线性……在卷积网络的背景下，并且已经发现它们可以提高区分性能。

当将ReLU与CNN一起使用时，它们可以用作过滤器映射本身的激活函数，然后是一个池层。

卷积网络的典型层由三个阶段组成……在第二阶段中，每个线性激活都经过非线性激活函数，例如校正后的线性激活函数。此阶段有时称为检测器阶段。

传统上，LSTM使用tanh激活函数来激活信元状态，并使用sigmoid激活函数来激活节点输出。考虑到它们的精心设计，ReLU被认为不适合默认的递归神经网络(RNN)，例如长期短期记忆网络(LSTM)。

乍一看，ReLU似乎不适合RNN，因为它们可以有非常大的输出，因此它们可能比有限制值的单元更有可能爆炸。

然而，已经有一些关于在LSTM中使用ReLU作为输出激活的研究工作，其结果是仔细初始化网络权重以确保网络在训练之前是稳定的。这一点在2015年题为“初始化线性校正单元的递归网络的简单方法”的论文中进行了概述。

尝试较小的偏移输入值

偏移是具有固定值的节点上的输入。

偏置具有移动激活函数的效果，并且传统的做法是将偏置输入值设置为1.0。

在网络中使用ReLU时，请考虑将偏移设置为较小的值，例如0.1。

……最好将[偏移]的所有元素设置为一个较小的正值，如0.1。这使得经过校正的线性单元很可能最初对于训练集中的大多数输入是有效的，并且允许导数通过。

关于是否需要这样做，有一些相互矛盾的报告，因此请将性能与偏置输入为1.0的模型进行比较。

使用“权重初始化”

在训练神经网络之前，必须将网络的权值初始化为较小的随机值。

在网络中使用RELU并将权重初始化为以零为中心的小随机值时，默认情况下，网络中一半的单位将输出零值。

例如，在统一初始化权重之后，大约50%的隐藏单元连续输出值是实数零。

有很多启发式方法来初始化神经网络的权值，但是除了权值初始化方案与激活函数的选择的一般准则之外，没有最优的权值初始化方案，几乎没有关系。

在ReLU被广泛采用之前，Xavier Glorot和Yoshua Bengio在他们2010年的论文《理解训练深度前馈神经网络的困难》中提出了一种初始化方案，该方案在使用sigmoid和tanh激活函数时迅速成为默认方案，通常被称为“Xavier Initialization”。权重设置为从与前一层中的节点数的大小成比例的范围内均匀采样的随机值(具体地说，+/- sqrt(2/n)，其中n是前一层中的节点数)。

何开明等人，在他们2015年发表的题为“深入研究整流器：在ImageNet分类上超越人类水平的性能”的论文中，他们建议Xavier初始化和其他方案不适合RELU和扩展。

Glorot和Bengio建议采用适当比例的均匀分布进行初始化。这称为“xavier”初始化……它的推导是基于激活是线性的假设。此假设对Relu无效。

他们建议对Xavier初始化进行较小的修改，使其适合与RELU一起使用，现在通常称为“He Initialization”(具体地说，+/-sqrt(2/n)，其中n是称为扇入的前一层中的节点数)。在实践中，该方案的高斯版本和均匀版本都可以使用。

缩放输入数据

在使用神经网络之前缩放输入数据是很好的做法。

这可能涉及将变量标准化为具有零均值和单位方差，或者将每个值归一化到0到1的范围。

在许多问题上没有数据缩放，神经网络的权值可能会变大，使网络变得不稳定，并增加泛化误差。

无论您的网络是否使用ReLU，这种扩展输入的良好实践都适用。

使用重量惩罚

通过设计，ReLU的输出在正域内是无界的。

这意味着在某些情况下，输出的大小可以继续增长。因此，使用某种形式的权重正则化(例如L1或L2向量范数)可能是个好主意。

由于激活的无界行为，可能会出现另一个问题；因此，人们可能希望使用正则化来防止潜在的数值问题。因此，我们对激活值使用L1惩罚，这也提升了额外的稀疏性。

这可以是促进稀疏表示(例如，使用L1正则化)和降低模型的泛化误差的良好实践。

ReLU的扩展和替代方案

ReLU确实有一些限制。

ReLU的限制中的关键是这样的情况，即较大的权重更新可能意味着激活函数的总和输入总是负的，而与网络的输入无关。

这意味着出现此问题的节点将永远输出激活值0.0。这被称为“濒临死亡的遗体”。

只要设备处于非激活状态，渐变就为0。这可能会导致单元从未激活的情况，因为基于梯度的优化算法不会调整最初从未激活的单元的权重。此外，就像消失梯度问题一样，当训练具有恒定0梯度的ReLU网络时，我们可能会期望学习会很慢。

REU的一些流行的扩展以某种方式放松了函数的非线性输出，以允许较小的负值。

Leaky ReLU(LReLU或LReL)修改函数，以便在输入小于零时允许较小的负值。

漏电整流器允许在装置饱和和不活动时出现小的非零梯度。

指数线性单位，或称ELU，是ReLU的推广，它使用参数化的指数函数从正值过渡到较小的负值。

ELU具有负值，这使得激活的平均值更接近于零。接近于零的平均激活使学习速度更快，因为它们使梯度更接近自然梯度。

参数ReLU或PReLU学习控制函数形状和泄漏性的参数。

……我们提出了ReLU的一种新的推广，我们称之为参数整流线性单元(PReLU)。该激活函数自适应地学习整流器的参数。

Maxout是一个可选的分段线性函数，它返回最大的输入，旨在与丢弃正则化技术结合使用。

我们定义了一个简单的新模型Maxout(之所以这样命名，是因为它的输出是一组输入中的最大值，而且因为它是辍学的天然伴侣)，其设计既便于通过辍学进行优化，又提高了辍学快速近似模型平均技术的精度。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

文章

如何使用校正后的线性激活函数修正消失梯度。

书籍

第6.3.1节纠正线性单位及其推广，深度学习，2016。

论文

API接口

max API

文章

0 0

Python