了解学习率对神经网络性能的影响

深度学习神经网络采用随机梯度下降优化算法进行训练。

学习率是控制每次更新模型权重时响应于估计误差而改变模型多少的超参数。选择学习率很有挑战性，因为太小的值可能会导致较长的训练过程，可能会卡住，而太大的值可能会导致学习次优的权重集太快或训练过程不稳定。

在配置神经网络时，学习率可能是最重要的超参数。因此，如何研究学习率对模型性能的影响，建立学习率动态变化对模型行为的直观认识是至关重要的。

在本教程中，你将了解学习速率、学习速率计划和自适应学习速率对模型性能的影响。

完成本教程后，你将了解：

  • 过大的学习率会导致训练不稳定，过小的学习率会导致训练失败。
  • 动量可以加速训练，而学习率时间表可以帮助收敛优化过程。
  • 自适应学习率可以加快训练速度，减轻选择学习率和学习率时间表的压力。

我们开始吧。

教程概述

本教程分为六个部分，它们是：

  • 学习率与梯度下降。
  • 以Keras为单位配置学习率。
  • 多类分类问题。
  • 学习速度和动量的影响。
  • 学习速度表的影响。
  • 适应性学习率的影响。

学习率与梯度下降

深度学习神经网络采用随机梯度下降算法进行训练。

随机梯度下降是一种优化算法，它使用训练数据集中的示例估计模型当前状态的误差梯度，然后使用误差反向传播算法(简称反向传播算法)更新模型的权重。

在训练期间更新权重的量称为步长或“学习率”。

具体地说，学习率是在神经网络的训练中使用的可配置的超参数，其具有小的正值，通常在0.0和1.0之间的范围内。

学习率控制模型适应问题的速度。考虑到每次更新对权重的改变较小，较小的学习率需要更多的训练周期，而较大的学习率会导致快速变化并且需要较少的训练周期。

太大的学习率可能会导致模型过快地收敛到次优解，而太小的学习率可能会导致过程停滞不前。

训练深度学习神经网络的挑战涉及仔细选择学习率。它可能是模型中最重要的超参数。

学习率可能是最重要的超参数。如果你只有时间调优一个超参数，请调优学习速率。

现在我们已经熟悉了学习率是多少，让我们来看看如何配置神经网络的学习率。

有关学习率及其工作原理的更多信息，请参见帖子：

以Keras为单位配置学习速率

Keras深度学习库允许你轻松配置随机梯度下降优化算法的多种不同变体的学习率。

随机梯度下降

Keras为实现随机梯度下降优化器的SGD类提供了学习率和动量。

首先，必须创建并配置类的实例，然后在对模型调用fit()函数时将其指定给“optimizer”参数。

默认学习速率为0.01，默认情况下不使用动量。

from keras.optimizers import SGD
...
opt = SGD()
model.compile(..., optimizer=opt)

学习率可以通过“lr”参数指定，动量可以通过“momentum”参数指定。

from keras.optimizers import SGD
...
opt = SGD(lr=0.01, momentum=0.9)
model.compile(..., optimizer=opt)

该类还通过“decay”参数支持学习率衰减。

在学习率衰减的情况下，每次更新(例如，每个小批次的结束)都会计算学习率，如下所示：

lrate = initial_lrate * (1 / (1 + decay * iteration))

其中，lrate是当前纪元的学习速率，initial_lrate是指定为SGD参数的学习速率，decay 是大于零的衰减率，迭代是当前更新编号。

from keras.optimizers import SGD
...
opt = SGD(lr=0.01, momentum=0.9, decay=0.01)
model.compile(..., optimizer=opt)

学习速度表。
KERAS通过回调支持学习速率计划。

回调独立于优化算法运行，尽管它们调整了优化算法使用的学习速率。建议在使用学习速率计划回调时使用SGD。

回调被实例化和配置，然后在训练模型时在列表中指定给fit()函数的“callback”参数。

Keras提供了ReduceLROnPlatform，它将在检测到模型性能的平台期时调整学习速率，例如，对于给定数量的训练周期没有变化。此回调旨在模型停止改进后降低学习率，希望微调模型权重。

ReduceLROnPlatform要求你通过“monitor”参数指定要在训练期间监视的指标，通过“factor”参数和“Patience”参数指定学习速率将乘以的值，“Patience”参数指定在触发学习速率更改之前等待的训练周期数。

例如，如果验证损失在100个时期内没有改善，我们可以监视验证损失，并将学习率降低一个数量级：

# snippet of using the ReduceLROnPlateau callback
from keras.callbacks import ReduceLROnPlateau
...
rlrop = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=100)
model.fit(..., callbacks=[rlrop])

Keras还提供了LearningRateScheduler回调，该回调允许你指定每个纪元调用的函数，以便调整学习速率。

你可以定义你的Python函数，该函数接受两个参数(Epoch和Current Learning Rate)并返回新的学习率。

# snippet of using the LearningRateScheduler callback
from keras.callbacks import LearningRateScheduler
...

def my_learning_rate(epoch, lrate):
	return lrate

lrs = LearningRateScheduler(my_learning_rate)
model.fit(..., callbacks=[lrs])

自适应学习率梯度下降

Keras还提供了一套支持自适应学习率的简单随机梯度下降的扩展。

因为每种方法都适应学习率(通常每个模型权重一个学习率)，所以通常只需要很少的配置。

三种常用的自适应学习速率方法包括：

RMSProp优化器

from keras.optimizers import RMSprop
...
opt = RMSprop()
model.compile(..., optimizer=opt)

Adagrad优化器

from keras.optimizers import Adagrad
...
opt = Adagrad()
model.compile(..., optimizer=opt)

ADAM优化器

from keras.optimizers import Adam
...
opt = Adam()
model.compile(..., optimizer=opt)

多类分类问题

我们将使用一个小的多类分类问题作为基础来演示学习率对模型性能的影响。

scikit-learn类提供make_blobs()函数，该函数可用于创建具有指定数量的样本、输入变量、类和类中样本的方差的多类分类问题。

该问题有两个输入变量(表示点的x和y坐标)和每个组内点的标准偏差2.0。我们将使用相同的随机状态(伪随机数生成器的种子)来确保始终获得相同的数据点。

# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

结果是我们可以建模的数据集的输入和输出元素。

为了了解问题的复杂性，我们可以在二维散点图上绘制每个点，并按类值对每个点进行着色。

下面列出了完整的示例。

# scatter plot of blobs dataset
from sklearn.datasets import make_blobs
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# scatter plot for each class value
for class_value in range(3):
	# select indices of points with the class label
	row_ix = where(y == class_value)
	# scatter plot for points with a different color
	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# show plot
pyplot.show()

运行该示例将创建整个数据集的散点图。我们可以看到，2.0的标准差意味着类不是线性可分的(可以用一条线分开)，这造成了许多模糊点。

这是可取的，因为它意味着问题不是微不足道的，并将允许神经网络模型找到许多不同的“足够好”的候选解决方案。

三类点按类值着色的BLOBS数据集散点图

学习速度和动量的影响

在这一部分，我们将开发一个多层感知器(MLP)模型来解决斑点分类问题，并研究不同学习率和动量的影响。

学习率动态

第一步是开发一个函数，该函数将从问题中创建样本，并将它们拆分成训练和测试数据集。

此外，我们还必须对目标变量进行热编码，以便我们可以开发预测属于每个类的示例的概率的模型。

下面的Prepare_Data()函数实现此行为，返回拆分为输入和输出元素的训练和测试集。

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

接下来，我们可以开发一个函数来拟合和评估MLP模型。

首先，我们将定义一个简单的MLP模型，该模型预期来自BLOBS问题的两个输入变量，具有一个具有50个节点的单个隐藏层，以及一个具有三个节点的输出层，以预测这三个类中的每一个的概率。隐藏层中的节点将使用校正的线性激活函数(ReLU)，而输出层中的节点将使用Softmax激活函数。

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))

我们将使用随机梯度下降优化器，并要求指定学习速率，以便我们可以评估不同的速率。该模型将被训练以最小化交叉熵。

# compile model
opt = SGD(lr=lrate)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

该模型适用于200个训练周期，试错次数较少，并将测试集作为验证数据集，对模型在训练过程中的泛化误差有一个初步的了解。

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

一旦符合，我们将在训练周期内绘制列车和测试集上模型的精确度。

# plot learning curves
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.title('lrate='+str(lrate), pad=-50)

下面的fit_model()函数将这些元素绑定在一起，它将拟合一个模型，并在给定训练和测试数据集以及要评估的特定学习率的情况下绘制其性能图。

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, lrate):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=lrate)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('lrate='+str(lrate), pad=-50)

现在我们可以研究不同学习率在列车上的动态变化，并测试模型的准确性。

在本例中，我们将在从1E-0(1.0)到1E-7的对数范围内评估学习速率，并通过调用fit_model()函数为每个学习速率创建线状图。

# create learning curves for different learning rates
learning_rates = [1E-0, 1E-1, 1E-2, 1E-3, 1E-4, 1E-5, 1E-6, 1E-7]
for i in range(len(learning_rates)):
	# determine the plot number
	plot_no = 420 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for a learning rate
	fit_model(trainX, trainy, testX, testy, learning_rates[i])
# show learning curves
pyplot.show()

将所有这些结合在一起，下面列出了完整的示例。

# study of learning rate on accuracy for blobs problem
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, lrate):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=lrate)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('lrate='+str(lrate), pad=-50)

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different learning rates
learning_rates = [1E-0, 1E-1, 1E-2, 1E-3, 1E-4, 1E-5, 1E-6, 1E-7]
for i in range(len(learning_rates)):
	# determine the plot number
	plot_no = 420 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for a learning rate
	fit_model(trainX, trainy, testX, testy, learning_rates[i])
# show learning curves
pyplot.show()

运行该示例将创建一个图形，其中包含针对八个不同评估学习速率的八个线条图。训练数据集上的分类精度标记为蓝色，而测试数据集上的分类精度标记为橙色。

由于学习算法的随机性，你的特定结果可能会有所不同。考虑将该示例运行几次。

曲线图显示了学习率1.0过大时的行为振荡，以及1E-6和1E-7学习率过低时模型无法学习任何东西。

可以看出，在1E-1、1E-2和1E-3的学习率下，模型能够很好地学习问题，但随着学习率的降低，学习速度逐渐变慢。在选择的模型配置下，结果表明，0.1的适度学习率会在训练和测试集上产生良好的模型性能。

斑点分类问题一组学习率的训练曲线图和测试精度

动量动力学

动量可以平滑学习算法的进程，而学习算法反过来又可以加速训练过程。

我们可以采用上一节中的例子来评估具有固定学习率的动量效应。在这种情况下，我们将选择上一节中收敛到合理解决方案的学习率0.01，但需要比学习率0.1更多的纪元。

可以将FIT_MODEL()函数更新为接受“Momentum”参数，而不是学习率参数，该参数可以在SGD类的配置中使用并报告结果图。

下面列出了此函数的更新版本。

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, momentum):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=momentum)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('momentum='+str(momentum), pad=-80)

通常使用接近1.0的动量值，例如0.9和0.99。

在此示例中，我们将演示没有动量的模型与动量值为0.5和更高的动量值的模型的动力学。

# create learning curves for different momentums
momentums = [0.0, 0.5, 0.9, 0.99]
for i in range(len(momentums)):
	# determine the plot number
	plot_no = 220 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for a momentum
	fit_model(trainX, trainy, testX, testy, momentums[i])
# show learning curves
pyplot.show()

将所有这些结合在一起，下面列出了完整的示例。

# study of momentum on accuracy for blobs problem
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, momentum):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, momentum=momentum)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('momentum='+str(momentum), pad=-80)

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different momentums
momentums = [0.0, 0.5, 0.9, 0.99]
for i in range(len(momentums)):
	# determine the plot number
	plot_no = 220 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for a momentum
	fit_model(trainX, trainy, testX, testy, momentums[i])
# show learning curves
pyplot.show()

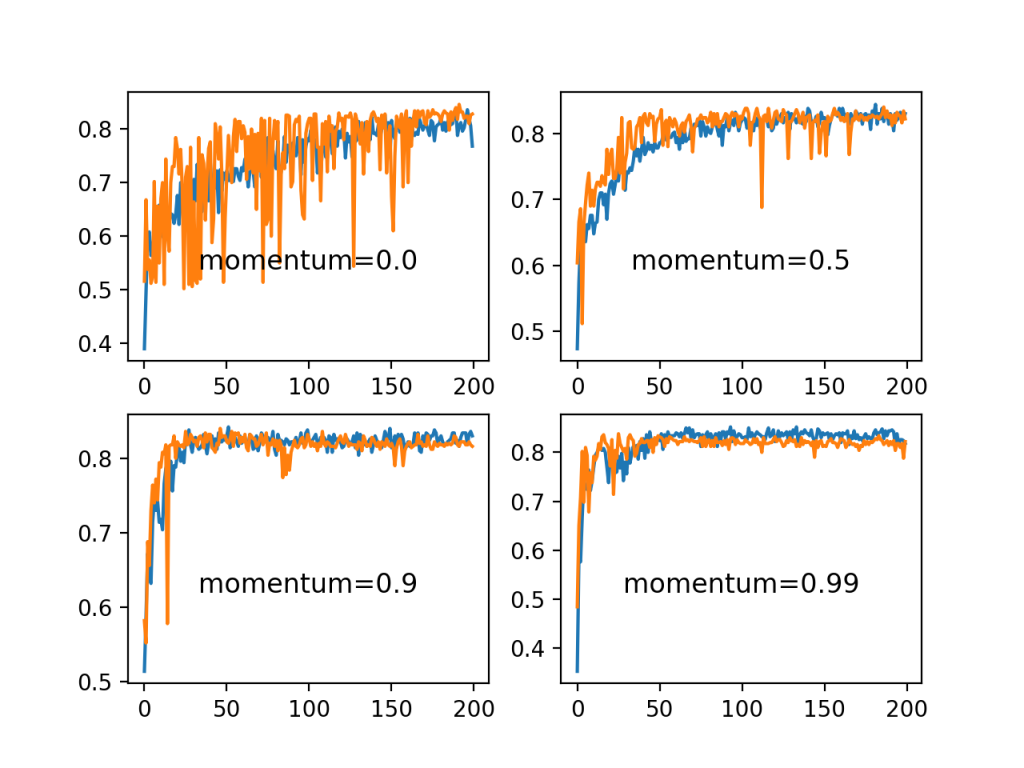
运行该示例将创建一个图形，该图形包含针对不同评估动量值的四个线状图。训练数据集上的分类精度标记为蓝色，而测试数据集上的分类精度标记为橙色。

由于学习算法的随机性，你的特定结果可能会有所不同。考虑将该示例运行几次。

我们可以看到，动量的增加确实加速了模型的训练。具体地说，动量值0.9和0.99在大约50个训练周期内实现了合理的训练和测试精度，而不是在不使用动量的情况下达到200个训练周期。

在使用动量的所有情况下，坚持测试数据集上的模型精度似乎更稳定，在训练期间显示出较小的波动性。

关于斑点分类问题的一组记忆的训练曲线图和测试精度
关于斑点分类问题的一组记忆的训练曲线图和测试精度

学习速度表的影响

在本节中，我们将查看两个学习速度表。

第一个是内置于SGD类中的衰退，第二个是ReduceLROnPlatform回调。

学习率衰减

SGD类提供指定学习速率衰减的“Decay”参数。

从方程或代码可能不清楚这种衰减对更新后的学习率的影响。我们可以用一个活生生的例子来更清楚地说明这一点。

下面的函数实现了SGD类中实现的学习率衰减。

# learning rate decay
def decay_lrate(initial_lrate, decay, iteration):
	return initial_lrate * (1.0 / (1.0 + decay * iteration))

我们可以使用此函数来计算具有不同衰减值的多次更新的学习率。

我们将比较衰减值范围[1E-1、1E-2、1E-3、1E-4]，初始学习率为0.01，权重更新为200。

decays = [1E-1, 1E-2, 1E-3, 1E-4]
lrate = 0.01
n_updates = 200
for decay in decays:
	# calculate learning rates for updates
	lrates = [decay_lrate(lrate, decay, i) for i in range(n_updates)]
	# plot result
	pyplot.plot(lrates, label=str(decay))

下面列出了完整的示例。

# demonstrate the effect of decay on the learning rate
from matplotlib import pyplot

# learning rate decay
def	decay_lrate(initial_lrate, decay, iteration):
	return initial_lrate * (1.0 / (1.0 + decay * iteration))

decays = [1E-1, 1E-2, 1E-3, 1E-4]
lrate = 0.01
n_updates = 200
for decay in decays:
	# calculate learning rates for updates
	lrates = [decay_lrate(lrate, decay, i) for i in range(n_updates)]
	# plot result
	pyplot.plot(lrates, label=str(decay))
pyplot.legend()
pyplot.show()

运行该示例将创建一个线状图，显示不同衰减值更新时的学习速率。

我们可以看到，在所有情况下，学习率都从初始值0.01开始。我们可以看到，小的衰减值1E-4(红色)几乎没有影响，而大的衰减值1E-1(蓝色)有很大的效果，在50个纪元内将学习率降低到0.002以下(大约比初始值低一个数量级)，最终达到0.0004左右(大约比初始值低两个数量级)。

我们可以看到，学习率的变化不是线性的。我们还可以看到，学习速率的更改取决于批大小，在批大小之后执行更新。在上一节的示例中，如果500个示例的默认批处理大小为32，则每个纪元有16个更新，200个纪元有3,200个更新。

使用0.1的衰减率和0.01的初始学习率，我们可以计算出最终的学习率是大约3.1E-05的一个很小的值。

多重权值更新时衰减对学习率影响的直线图

我们可以更新上一节中的示例，以评估不同学习率衰减值的动态变化。

将学习率固定在0.01并且不使用动量时，我们预计学习率衰减会非常小，因为很大的学习率衰减会很快导致学习率太小，以至于模型无法有效学习。

可以更新Fit_model()函数以接受“Decay”参数，该参数可用于配置SGD类的Decay。

下面列出了该函数的更新版本。

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, decay):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, decay=decay)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('decay='+str(decay), pad=-80)

我们可以评估[1E-1，1E-2，1E-3，1E-4]的相同四个衰减值及其对模型精度的影响。

下面列出了完整的示例。

# study of decay rate on accuracy for blobs problem
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, decay):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01, decay=decay)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('decay='+str(decay), pad=-80)

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different decay rates
decay_rates = [1E-1, 1E-2, 1E-3, 1E-4]
for i in range(len(decay_rates)):
	# determine the plot number
	plot_no = 220 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for a decay rate
	fit_model(trainX, trainy, testX, testy, decay_rates[i])
# show learning curves
pyplot.show()

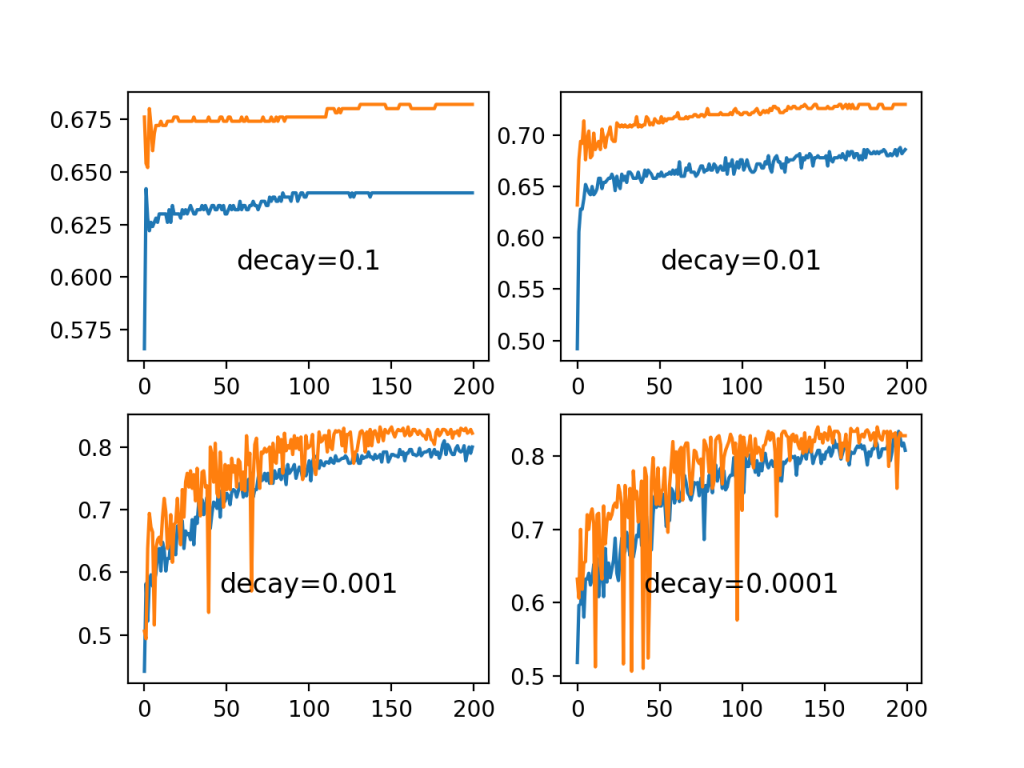
运行该示例将创建一个图形，该图形包含针对不同评估的学习率衰减值的四个线状图。训练数据集上的分类精度标记为蓝色，而测试数据集上的分类精度标记为橙色。

由于学习算法的随机性，你的特定结果可能会有所不同。考虑将该示例运行几次。

可以看出，1E-1和1E-2的较大衰减值确实使该模型在这个问题上的学习速率衰减得太快，导致性能较差。衰减值越大性能越好，值1E-4可能会导致与根本不使用衰退类似的结果。事实上，我们可以计算出衰减为1E-4的最终学习率约为0.0075，仅比初值0.01%略小一点。

斑点分类问题中一组衰减率的训练曲线图和测试精度
斑点分类问题中一组衰减率的训练曲线图和测试精度

高原地区的学习速度下降

ReduceLROnPlatform在监视的度量在给定的历元数内没有变化之后，将使学习率下降一个因子。

我们可以探索不同的“耐心”值的影响，“耐心”值是在降低学习率之前等待改变的时代数。我们将使用默认学习率0.01，并通过将“factor”参数设置为0.1将学习率降低一个数量级。

rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7)

回顾培训期间对学习率的影响将是一件有趣的事情。我们可以通过创建一个新的Kera回调来实现这一点，该回调负责记录每个训练周期结束时的学习速率。然后，我们可以检索记录的学习率，并创建一张曲线图，以查看学习率是如何受到水滴的影响的。

我们可以创建一个名为LearningRateMonitor的自定义回调。On_Train_Begin()函数在训练开始时调用，在其中我们可以定义一个空的学习率列表。Onpechend()函数在每个训练周期结束时调用，在该函数中，我们可以从优化器检索优化器和当前的学习率，并将其存储在列表中。下面列出了完整的LearningRateMonitor回调。

# monitor the learning rate
class LearningRateMonitor(Callback):
	# start of training
	def on_train_begin(self, logs={}):
		self.lrates = list()

	# end of each training epoch
	def on_epoch_end(self, epoch, logs={}):
		# get and store the learning rate
		optimizer = self.model.optimizer
		lrate = float(backend.get_value(self.model.optimizer.lr))
		self.lrates.append(lrate)

可以更新前几节中开发的fit_model()函数，以创建和配置ReduceLROnPlatform回调和我们新的LearningRateMonitor回调，并将它们注册到FIT调用中的模型中。

该函数还将“patience”作为参数，以便我们可以评估不同的值。

# fit model
rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7)
lrm = LearningRateMonitor()
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm])

在本例中，我们希望创建几个曲线图，因此Fit_model()函数将返回每个训练时期的学习速率列表以及训练数据集上的损失和精度，而不是直接创建子曲线图。

下面列出了具有这些更新的函数。

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, patience):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7)
	lrm = LearningRateMonitor()
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm])
	return lrm.lrates, history.history['loss'], history.history['accuracy']

ReduceLROnPlatform中的耐心控制学习速率下降的频率。

我们将在BLOBS问题上测试适合此模型的几个不同的耐心值，并跟踪每次运行的学习率、损失和准确率系列。

# create learning curves for different patiences
patiences = [2, 5, 10, 15]
lr_list, loss_list, acc_list, = list(), list(), list()
for i in range(len(patiences)):
	# fit model and plot learning curves for a patience
	lr, loss, acc = fit_model(trainX, trainy, testX, testy, patiences[i])
	lr_list.append(lr)
	loss_list.append(loss)
	acc_list.append(acc)

在运行结束时，我们将为每个耐心值创建数字，其中包括每个耐心值的学习率、训练损失和训练精确度。

我们可以创建一个helper函数来轻松地为我们记录的每个系列创建一个带有子图的图形。

# create line plots for a series
def line_plots(patiences, series):
	for i in range(len(patiences)):
		pyplot.subplot(220 + (i+1))
		pyplot.plot(series[i])
		pyplot.title('patience='+str(patiences[i]), pad=-80)
	pyplot.show()

将这些元素捆绑在一起，完整的示例如下所示。

# study of patience for the learning rate drop schedule on the blobs problem
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from keras.callbacks import Callback
from keras.callbacks import ReduceLROnPlateau
from keras import backend
from matplotlib import pyplot

# monitor the learning rate
class LearningRateMonitor(Callback):
	# start of training
	def on_train_begin(self, logs={}):
		self.lrates = list()

	# end of each training epoch
	def on_epoch_end(self, epoch, logs={}):
		# get and store the learning rate
		optimizer = self.model.optimizer
		lrate = float(backend.get_value(self.model.optimizer.lr))
		self.lrates.append(lrate)

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, patience):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	opt = SGD(lr=0.01)
	model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
	# fit model
	rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7)
	lrm = LearningRateMonitor()
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm])
	return lrm.lrates, history.history['loss'], history.history['accuracy']

# create line plots for a series
def line_plots(patiences, series):
	for i in range(len(patiences)):
		pyplot.subplot(220 + (i+1))
		pyplot.plot(series[i])
		pyplot.title('patience='+str(patiences[i]), pad=-80)
	pyplot.show()

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different patiences
patiences = [2, 5, 10, 15]
lr_list, loss_list, acc_list, = list(), list(), list()
for i in range(len(patiences)):
	# fit model and plot learning curves for a patience
	lr, loss, acc = fit_model(trainX, trainy, testX, testy, patiences[i])
	lr_list.append(lr)
	loss_list.append(loss)
	acc_list.append(acc)
# plot learning rates
line_plots(patiences, lr_list)
# plot loss
line_plots(patiences, loss_list)
# plot accuracy
line_plots(patiences, acc_list)

运行该示例将创建三个图形，每个图形都包含不同耐心值的线图。

由于学习算法的随机性，你的特定结果可能会有所不同。考虑将该示例运行几次。

第一张图显示了每个评估的耐心值在训练期间的学习率的线状图。我们可以看到，最小的耐心值2会使学习率在25个时代内迅速下降到最小值，而最大的耐心值15只会使学习率下降一次。

从这些图中，我们预计这个模型在这个问题上的耐心值为5和10将导致更好的性能，因为它们允许在放弃速率以优化权重之前使用较大的学习率一段时间。

ReduceLROnPlatform计划中使用的不同耐心值的历时学习速率曲线图

下图显示了每个耐心值在训练数据集上的损失。

图中显示，耐心值为2和5会导致模型快速收敛，可能会收敛到次优损失值。在耐心水平为10和15的情况下，损失会合理地下降，直到学习率降到可以看到损失的巨大变化的水平以下。这在耐心10的中途发生，在耐心15的奔跑接近尾声。

ReduceLROnPlatform计划中使用的不同耐心值在历时内的训练损失曲线图

最后的数字显示了每个耐心值在训练时段内的训练集精度。

我们可以看到，事实上，2和5个历元的小耐心值导致模型过早收敛到精度分别在65%和75%左右的非最优模型。耐心值越大，模型的性能越好，耐心10显示恰好在150个历元之前的收敛，而耐心15继续显示在学习率几乎完全不变的情况下不稳定精度的影响。

这些曲线图显示了降低的学习率是如何以一种合理的方式解决问题和选择的模型配置，可以导致熟练且收敛的稳定的最终权重集，这是培训运行结束时最终模型中的理想属性。

ReduceLROnPlatform计划中使用的不同耐心值在历元上的训练精度的曲线图

适应性学习率的影响

学习速率和学习速率调度对于深度学习神经网络模型的性能来说，既是具有挑战性的配置，也是至关重要的。

KERAS提供了许多具有自适应学习率的随机梯度下降的不同流行变体，例如：

  • 自适应梯度算法(AdaGrad)。
  • 均方根传播(RMSprop)。
  • 自适应矩估计(ADAM)。

每种方法都为调整网络中每个权重的学习率提供了不同的方法。

没有单一的最优算法，赛车优化算法在一个问题上的结果不太可能转移到新的问题上。

我们可以研究不同的自适应学习速率方法在BLOBS问题上的动态特性。可以更新fit_model()函数以获取要计算的优化算法的名称，该名称可以在编译MLP模型时指定给“Optimizer”参数。然后将使用每个方法的默认参数。下面列出了该函数的更新版本。

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, optimizer):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('opt='+optimizer, pad=-80)

我们可以探索RMSprop、AdaGrad和Adam这三种流行的方法，并将它们的行为与具有静态学习率的简单随机梯度下降进行比较。

我们希望算法的自适应学习率版本的性能类似或更好，可能在更少的训练时间内适应问题，但重要的是，会产生更稳定的模型。

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different optimizers
momentums = ['sgd', 'rmsprop', 'adagrad', 'adam']
for i in range(len(momentums)):
	# determine the plot number
	plot_no = 220 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for an optimizer
	fit_model(trainX, trainy, testX, testy, momentums[i])
# show learning curves
pyplot.show()

将这些元素捆绑在一起，完整的示例如下所示。

# study of sgd with adaptive learning rates in the blobs problem
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from keras.callbacks import Callback
from keras import backend
from matplotlib import pyplot

# prepare train and test dataset
def prepare_data():
	# generate 2d classification dataset
	X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
	# one hot encode output variable
	y = to_categorical(y)
	# split into train and test
	n_train = 500
	trainX, testX = X[:n_train, :], X[n_train:, :]
	trainy, testy = y[:n_train], y[n_train:]
	return trainX, trainy, testX, testy

# fit a model and plot learning curve
def fit_model(trainX, trainy, testX, testy, optimizer):
	# define model
	model = Sequential()
	model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
	model.add(Dense(3, activation='softmax'))
	# compile model
	model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
	# fit model
	history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)
	# plot learning curves
	pyplot.plot(history.history['accuracy'], label='train')
	pyplot.plot(history.history['val_accuracy'], label='test')
	pyplot.title('opt='+optimizer, pad=-80)

# prepare dataset
trainX, trainy, testX, testy = prepare_data()
# create learning curves for different optimizers
momentums = ['sgd', 'rmsprop', 'adagrad', 'adam']
for i in range(len(momentums)):
	# determine the plot number
	plot_no = 220 + (i+1)
	pyplot.subplot(plot_no)
	# fit model and plot learning curves for an optimizer
	fit_model(trainX, trainy, testX, testy, momentums[i])
# show learning curves
pyplot.show()

运行该示例将创建一个图形，该图形包含用于不同评估的优化算法的四个线状图。训练数据集上的分类精度标记为蓝色，而测试数据集上的分类精度标记为橙色。

由于学习算法的随机性，你的特定结果可能会有所不同。考虑将该示例运行几次。

同样，我们可以看到，默认学习率为0.01且没有动量的SGD确实学习了问题，但几乎需要所有200个历元，并导致训练数据的准确性不稳定，在测试数据集上更是如此。实验结果表明，三种自适应学习率方法学习问题的速度都较快，训练和测试集精度的波动性明显较小。

RMSProp和ADAM都表现出类似的性能，在50个训练周期内有效地学习了问题，并将剩余的训练时间花费在非常小的权重更新上，但不像我们在上一节中看到的学习速率时间表那样收敛。

斑点分类问题一套自适应学习率方法的训练曲线和测试精度

进一步阅读

如果你想深入了解，本节提供了更多关于该主题的资源。

文章

论文

书籍

API接口

文章

00

Python

发表评论

邮箱地址不会被公开。 必填项已用*标注

什么阻碍了你实现迈入机器学习领域的目标？

什么阻碍了你实现迈入机器学习领域的目标？

2020-04-22 机器学习

如果你在为进入机器学习领域而挣扎，感觉到有什么东西阻止了自己的开始，那么你应该看看这篇文章。 在这篇文章中，我们会讨论阻止进入机器学习领域的自我限制的信念，让你明白面临的问题。 几乎总是一种自我限制的信念阻碍了你们的进步。 也许你会在一个或多个这样的信念中看到自己。如果是这样的话， [......]

了解详情

机器学习入门

R语言机器学习迷你课程

R语言机器学习迷你课程

2020-08-12 机器学习

在这个迷你课程中，你将发现如何开始，构建精确的模型，并自信地完成在14天内使用R预测建模机器学习项目。 这是一个重要而重要的文章。你可能想把它书签。 了解如何准备数据，拟合机器学习模型，并用我的新书评估他们在r上的预测，包括14步教程、3个项目和完整源代码。 我们开始吧。 [......]

了解详情

机器学习入门

关于机器学习的几点思考

关于机器学习的几点思考

2020-04-26 机器学习

机器学习是一个大的、跨学科的研究领域。 你可以通过机器学习获得令人印象深刻的结果，并找到非常具有挑战性的问题的解决方案。但这只是更广泛的机器学习领域的一小部分，通常被称为预测建模或预测分析。 在这篇文章中，你将发现如何改变你对机器学习的思考方式，以便更好地为你提供机器学习实践者的服务。 [......]

了解详情

机器学习入门

找到你的机器学习部落

找到你的机器学习部落

2020-04-26 机器学习

机器学习是一个充满算法和数据的迷人而强大的研究领域。 问题是，有这么多不同类型的人对机器学习感兴趣，每个人都有不同的需求。重要的是要了解你想要从机器学习中得到什么，并根据这些需求调整你的自学。 如果你不这样做，你很容易就会陷入困境，迷失方向，失去兴趣，得不到你想要的东西。 找到 [......]

了解详情

机器学习入门

应用机器学习过程

应用机器学习过程

2020-04-26 机器学习

随着时间的推移，在处理应用机器学习问题时，你会开发出一种模式或流程，以快速获得良好的正常结果。 一旦开发完成，你就可以在一个又一个项目上反复使用此过程。你的流程越健壮、越发达，你就能越快地获得可靠的结果。 在这篇文章中，我想与你分享我解决机器学习问题的过程框架。 你可以将其用作下一 [......]

了解详情

机器学习入门

机器学习中的向量范数介绍
机器学习中的向量范数介绍
如何用Keras进行预测
如何用Keras进行预测
机器学习中的交叉熵介绍
机器学习中的交叉熵介绍
在Keras中显示深度学习模型训练历史
在Keras中显示深度学习模型训练历史

你或许会喜欢

如何用Anaconda构建机器学习和深度学习的Python环境
关于机器学习的几点思考
WEKA高级用法
Python机器学习迷你课程
浅谈小批量梯度下降及批量配置
WEKA入门
如何从头开始开发CIFAR-10照片分类的CNN
为什么机器学习领域不会太难?